Program Scilab
Rozwiązywanie układów równań liniowych. Układ równań
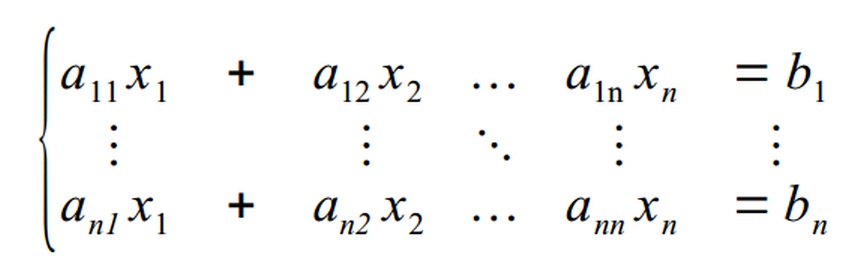 możemy za pomocą macierzy (tablicy) $A$ rozmiaru $n\times n$ oraz wektorów jednokolumnowych $x$ i $b$
możemy za pomocą macierzy (tablicy) $A$ rozmiaru $n\times n$ oraz wektorów jednokolumnowych $x$ i $b$
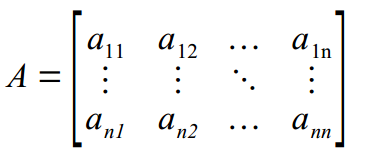
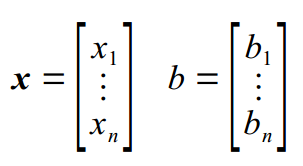 zapisać w postaci $A\cdot x=b$. Zapis ten sugeruje, że aby otrzymać $x$ trzeba $b$ podzielić przez $A$. Rzeczywiście, rozwiążemy układ: $$\begin{cases}x+y+z=6\\x+y-z=0\\x-y-z=-4\end{cases}$$
zapisać w postaci $A\cdot x=b$. Zapis ten sugeruje, że aby otrzymać $x$ trzeba $b$ podzielić przez $A$. Rzeczywiście, rozwiążemy układ: $$\begin{cases}x+y+z=6\\x+y-z=0\\x-y-z=-4\end{cases}$$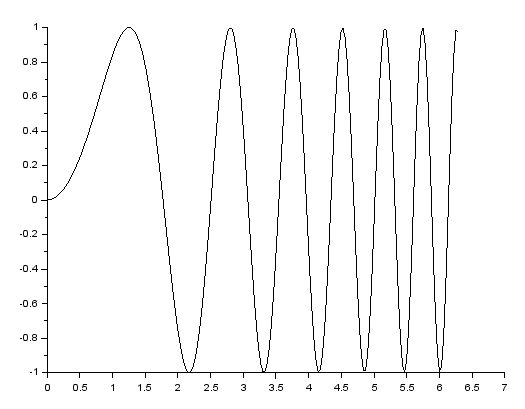 Polecenie rysujące plot2d dostaje tylko ciąg punktów, nie dostaje informacji jak ten ten ciąg powstał, nie może zatem opisać wykresu. O opisanie wykresu musi zadbać użytkownik programu.
Polecenie rysujące plot2d dostaje tylko ciąg punktów, nie dostaje informacji jak ten ten ciąg powstał, nie może zatem opisać wykresu. O opisanie wykresu musi zadbać użytkownik programu.
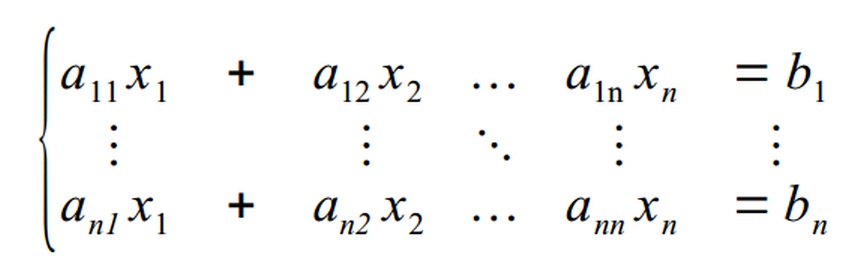
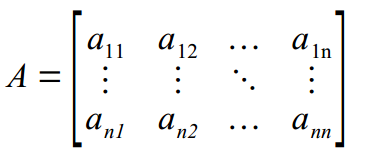
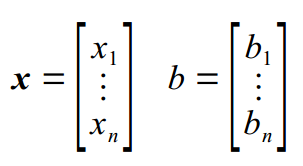
A = [1 1 1;1 1 -1;1 -1 -1] b = [6 0 -4]' x = (A\b)' ⇒ 1. 2. 3.Dwukrotnie odbyła się transpozycja: wektor $b$ musi być kolumnowy, rozwiązanie chciałem wyświetlić w jednym wierszu.
Obliczanie pierwiastków wielomianu. W programie Scilab wielomiany tworzymy poleceniem poly(A,zm,[flaga]), gdzie $A$ jest jednowierszową tablicą liczb, $zm$ jest symbolem zmiennej, nieobowiązkowy parametr $flaga$ decyduje czy liczby z wektora $A$ są współczynnikami wielomianu (flaga='c'), czy pierwiastkami (flaga='r'). Domyślnie są pierwiastkami. Do obliczenia pierwiastków wielomianu $w$ służy polecenie roots(w).
A = 1:5 ⇒ 1. 2. 3. 4. 5.
w = 0.5*poly(A,'y','c') ⇒ 0.5 + y + 1.5y2 + 2y3 + 2.5y4
roots(w) ⇒
0.1378323 + 0.6781544i
0.1378323 - 0.6781544i
- 0.5378323 + 0.3582847i
- 0.5378323 - 0.3582847i
Wszystkie pierwiastki są zespolone.
Sporządzanie wykresów funkcji jednej zmiennej. Rysujemy poleceniem plot2d(wektor_x,wektor_y), wektor_x i wektor_y muszą być wektorami tej samej długości. Wykres funkcji $y=\sin(x^2)$ na przedziale $[0,2\cdot\pi]$ uzyskujemy tak:
x = linspace(0,2*%pi,201); y = sin(x.*x); plot2d(x,y)
