Scilab

Utwórz tablicę $A$ o rozmiarze $10000\times 2$, o takiej zawartości: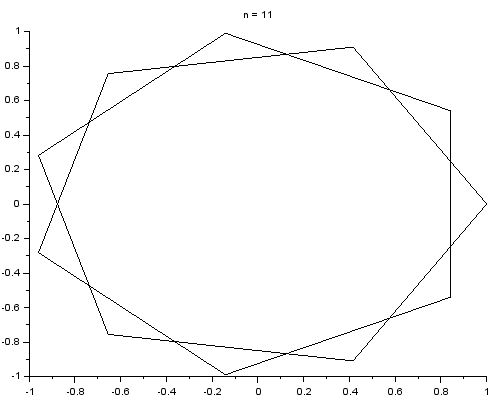

1         0.2224478
1001      0.4957695
2001      0.4998512
3001      0.5056818
...
98001     0.5007329
99001     0.500273
10000     0.4991944

Jeżeli $n$ oznacza liczbę w pierwszej kolumnie, to liczba w drugiej kolumnie jest średnią arytmetyczną $n$ losowo wybranych liczb z przedziału [0,1). Przydatna może być funkcja mean(A) wyliczająca średnią wartość liczb z tablicy $A$.

Rozwiązanie

A = []
for i = 1:10000
  A = [A [i;mean(rand(i,1))]]
end
A = A'

Zaczynamy od pustej tablicy ($A=[]$), potem w pętli dopisujemy z prawej strony tablicę o rozmiarze $2\times 1$.

Ukryj

Utwórz tablicę $B$ o rozmiarze $3\times 101$.

Pierwszy wiersz ma zawierać 101 wylosowanych liczb całkowitych z przedziału $[0,1000]$.
Drugi wiersz ma zawierać liczby z pierwszego wiersza uporządkowane malejąco.
Trzeci wiersz ma zawierać liczby z pierwszego wiersza uporządkowane rosnąco.

Wypisz medianę liczb z pierwszego wiersza.

Rozwiązanie

B = floor(1001*rand(1,101))
A = [B;gsort(B);gsort(B,'g','i')]
disp(A(2,51))

Funkcja rand(1,101) utworzy tablicę o rozmiarze $1\times 101$ zawierającą liczby losowe z przedziału $[0,1)$. Po pomnożeniu przez $1001$ i zaokrągleniu w dół dostaniemy liczby całkowite z przedziału $[0,1000]$. Funkcja gsort bez parametrów sortuje malejąco, a z parametrami rosnąco. Sortowanie nie ma wpływu na wartość mediany, a po sortowaniu mediana jest w środku wektora.

Ukryj

Utwórz tablicę $C$ o rozmiarze $100\times 100$, taką, że liczba w wierszu $w$ i kolumnie $k$ ma wartość $w^2+k^2$.

Rozwiązanie

x = (1:100).*(1:100);
y = x;
x = x';
C = [];
for i = 1:length(y)
  C = [C y(i)+x];
end

Po utworzeniu, tablica $x$ jest jednowierszowa i zawiera kwadraty liczb całkowitych z przedziału $[1,100]$. Taką samą zawartość ma tablica $y$. W trzecim wierszu kodu, tablica $x$ staje sie (nie zmieniając zawartości) tablica jednokolumnową.

Ukryj

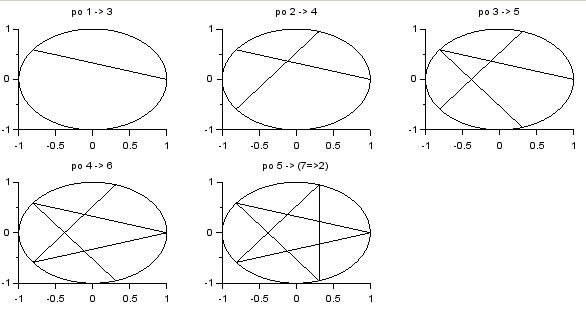
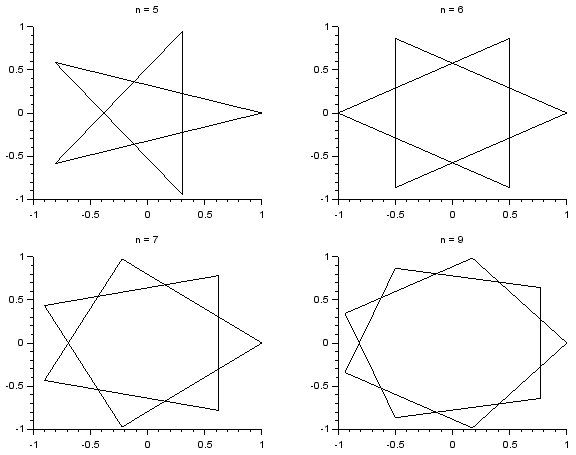
Napisz skrypt, który rysuje foremne wielokąty gwiaździste typu {n/2} (o wartość $n$ skrypt pyta użytkownika). Wielokąt foremny typu {n/2} powstaje przez połączenie co drugiego wierzchołka w zwykłym n-kącie foremnym.

Rozwiązanie

disp("Wielokąty gwiaździste (n,2)")
n = input("n = ")
t = linspace(0,2*%pi,n+1)
x = cos(t)
y = sin(t)
for i = 1:n
   next = i+2
   if (next > n+1) 
      next = 2
   end    
   plot2d([x(i) x(next)],[y(i) y(next)])
end
xtitle("n = "+string(n))

Zaczynamy od obliczenia współrzędnych wierzchołków (instrukcje t = ..., x = ..., y = ...). Następnie rysujemy odcinki łączące wierzchołki o numerach $i$ oraz $i+2$, kłopot pojawia się pod koniec – wektory mogą nie mieć współrzędnej o numerze $i+2$.

Po zapisaniu skryptu po nazwą polygons.sce w katalogu roboczym Scilaba, wpisaniu na konsoli kodu

for k = 1:4
    subplot(2,2,k)
    exec('polygons.sce',-1)
end

i udzieleniu kolejno odpowiedzi $5,6,7,9$ otrzymamy taki rysunek:

Ukryj