Scilab

Poniższy kod rysuje spiralę Archimedesa – krzywą o równaniu $r=\phi$ (we współrzędnych biegunowych).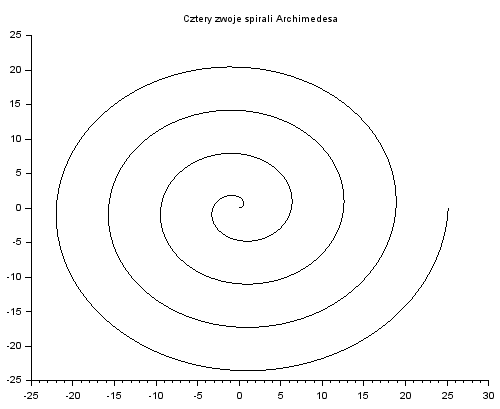

t = linspace(0,8*%pi,401); 
x = t.*cos(t); 
y = t.*sin(t);
plot2d(x,y)
xtitle("Cztery zwoje spirali Archimedesa") ⇒

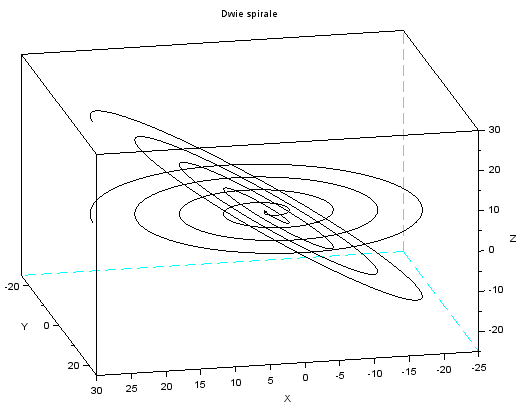
Narysuj w przestrzeni dwie spirale, jedna leży w płaszczyźnie $Oxy$ i jest krzywą z powyższego przykładu. Druga leży w płaszczyźnie o równaniu $z=x$, a jej rzutem na płaszczyznę $Oxy$ jest pierwsza krzywą.

Rozwiązanie

t = linspace(0,8*%pi,401); 
x = t.*cos(t); 
y = t.*sin(t);
param3d(x,y,zeros(x))
param3d(x,y,x)
xtitle("Dwie spirale") ⇒

Ukryj

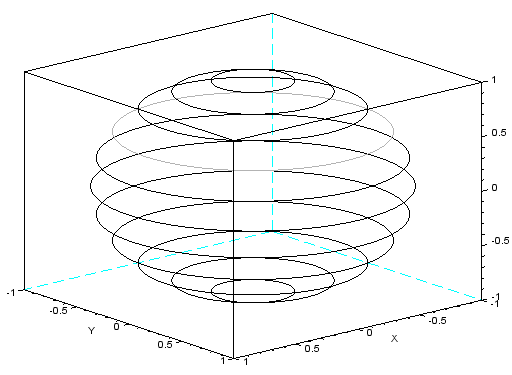
Narysuj poniższą figurę – równoleżniki oddalone od siebie o 15° szerokości geograficznej.

Rozwiązanie

t = linspace(0,2*%pi,201);
x = cos(t);
y = sin(t);
for fi = linspace(-90,90,13)
  param3d(cosd(fi)*x,cosd(fi)*y,sind(fi)*ones(x))
end

Funkcje trygonometryczne $cosd$ i $sind$ oczekują argumentu w stopniach. Funkcja ones(tab) tworzy tablicę wypełnioną jedynkami o takim samym rozmiarze jak $tab$.

Ukryj

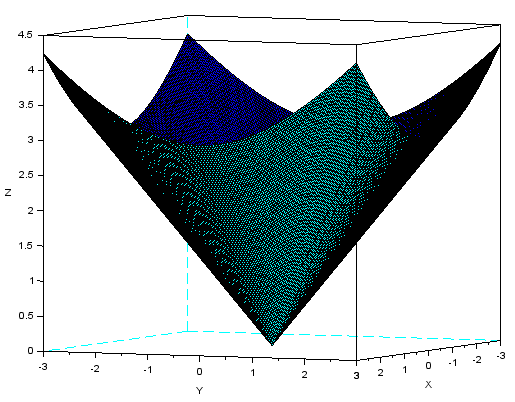
Narysuj odwócony stożek.

Rozwiązanie

Odwrócony stożek ma równanie $z=a\cdot\sqrt{x^2+y^2},\,\,a\gt 0$, wybierzmy $a=1$.

x = linspace(-4,4,201);
y = x;
z = zeros(201,201);
for w = 1:201
  for k = 1:201
    z(w,k) = sqrt(x(w)^2 + y(k)^2);
  end
end
plot3d(x,y,z)

Ukryj