Program Scilab
Rysowanie krzywych.
Rysujemy poleceniem param3d(wektor_x,wektor_y,wektor_z), wektory będące argumentami funkcji param3d muszą mieć taką samą długość. Takie podejście do rysowania wynika z tego, że krzywe w przestrzeni opisywane są zawyczaj parametrycznie $$\begin{cases}x=f_1(t)\\y=f_2(t)\\z=f_3(t)\end{cases}$$ Wpierw przygotowujemy wektor parametrów $t$, następnie wyliczamy współrzędne wektorów $x$, $y$ i $z$.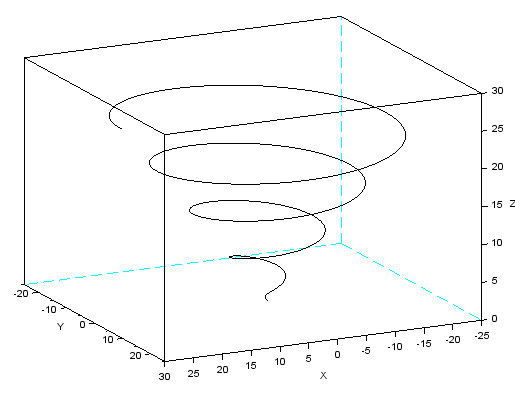 Rysunki trójwymiarowe w Scilabie można obracać (prawy przycisk myszy), powyższy wygląd narysowana krzywa uzyskała po wykonaniu obrotu.
Rysunki trójwymiarowe w Scilabie można obracać (prawy przycisk myszy), powyższy wygląd narysowana krzywa uzyskała po wykonaniu obrotu.
Sporządzenie wykresu funkcji $z=\frac{\sin(x^2+y^2)}{x^2+y^2},\,\,x,y\in [-6,6]$.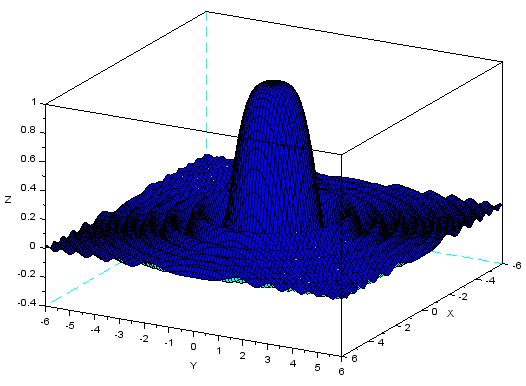
Rysujemy poleceniem param3d(wektor_x,wektor_y,wektor_z), wektory będące argumentami funkcji param3d muszą mieć taką samą długość. Takie podejście do rysowania wynika z tego, że krzywe w przestrzeni opisywane są zawyczaj parametrycznie $$\begin{cases}x=f_1(t)\\y=f_2(t)\\z=f_3(t)\end{cases}$$ Wpierw przygotowujemy wektor parametrów $t$, następnie wyliczamy współrzędne wektorów $x$, $y$ i $z$.
t = linspace(0,8*%pi,601); x = t.*cos(t); y = t.*sin(t); z = t; param3d(x,y,z) ⇒

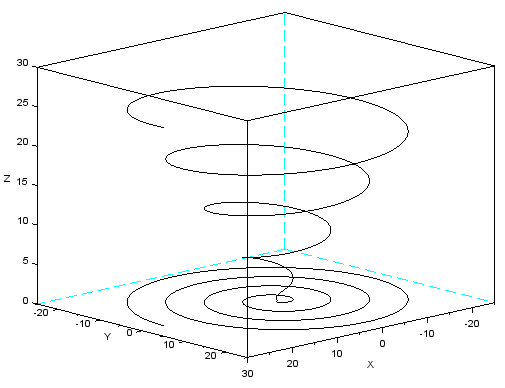
Uzupełnimy rysunek o rzut krzywej na płaszczyznę $Oxy$. Funkcja zeros(tab) tworzy tablicę (wektor) o takim samym wymiarze jak tab, wypełnioną zerami.
param3d(x,y,zeros(z)) ⇒

Podobnie do polecenia plot2d, polecenie param3d rysuje w rzeczywistości łamaną.
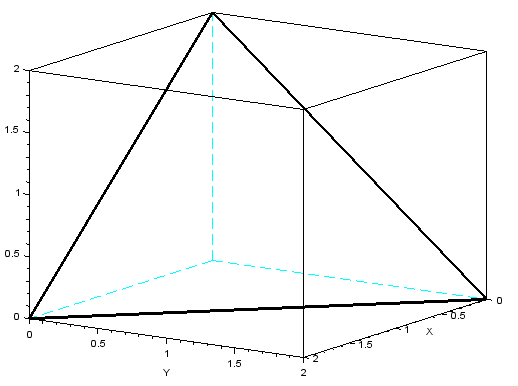
x = [2 0 0 2]
y = [0 2 0 0]
z = [0 0 2 0]
set("thickness",3)
param3d(x,y,z) ⇒ osie i krzywa sa pogrubione
set("thickness",1) ⇒ przywraca cienkość osi

Rysowanie powierzchnii.
Rysujemy poleceniem plot3d(wektor_x,wektor_y,values_xy), długości wektorów wektor_x i wektor_y nie muszą byc równe, tablica values_xy musi mieć rozmiar $n_x\times n_y$, gdzie $n_x$
jest długością wektora wektor_x, a $n_y$ jest długością wektora wektor_y.
Sporządzenie wykresu funkcji $z=x^2+y^2,\,\,x,y\in [-2,2]$.
x = linspace(-2,2,201);
y = x;
z = zeros(201,201);
for w = 1:length(y)
for k = 1:lenght(x)
z(w,k) = y(w)^2 + x(k)^2;
end
end
plot3d(x,y,z)
Jeżeli wzór na funkcję jest skomplikowany, to dla skrócenia zapisu warto zdefiniować własną funkcję.
Sporządzenie wykresu funkcji $z=\frac{\sin(x^2+y^2)}{x^2+y^2},\,\,x,y\in [-6,6]$.
function [w] = h(a,b)
pom = a.*a + b.*b
w = sin(pom)./pom
endfunction
x = linspace(-6,6,100);
y = linspace(-6,6,100);
z = zeros(100,100);
for w = 1:100
for k = 1:100
z(w,k) = h(x(w),y(k));
end
end
plot3d(x,y,z) ⇒
