Program Scilab

Wszystkie dotychczasowe rysunki były wykresami funkcji $y=f(x)$. Wynikało to ze sposobu przygotowania danych dla polecenia plot2d(x,y) – wektor $x$ tworzony poleceniem linspace(...) jest rosnący. Możliwe są też inne rysunki.

Krzywa parametryczna, tzn. krzywa opisana równaniami $\begin{cases}x=f(t)\\y=g(t)\end{cases}$.
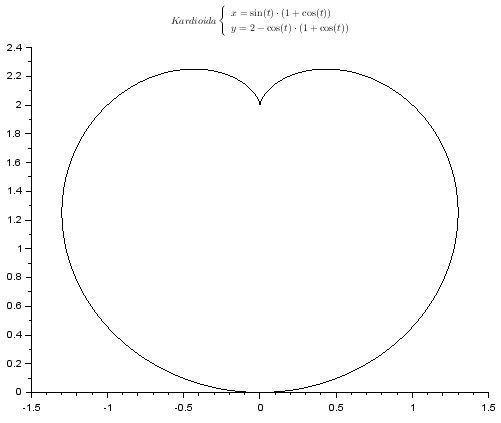
Przykład krzywej parametrycznej (kardioida):

t = linspace(0,2*%pi,301);
x = sin(t).*(1+cos(t));
y = 2-cos(t).*(1+cos(t));
plot2d(x,y)
xtitle("$Kardioida \begin{cases}x=\sin(t)\cdot (1+\cos(t))\\y=2-\cos(t)\cdot(1+\cos(t))\end{cases}$") ⇒

Geometryczna definicja kardioidy – krzywa zakreślana przez ustalony punkt okręgu toczącego się po zewnętrzu innego okręgu.
Polecenie xtitle("tytuł") wyświetla tytuł nad rysunkiem i jak widać, akceptuje składnię LaTeXa.

W rzeczywistości, polecenie plot2d(x,y) rysuje łamaną: zaznacza opisane w wektorach $x$ i $y$ punkty i łączy je odcinkami. Jeśli punktów jest dużo, to segmenty łamanej są krótkie i widzimy ją w postaci krzywej.
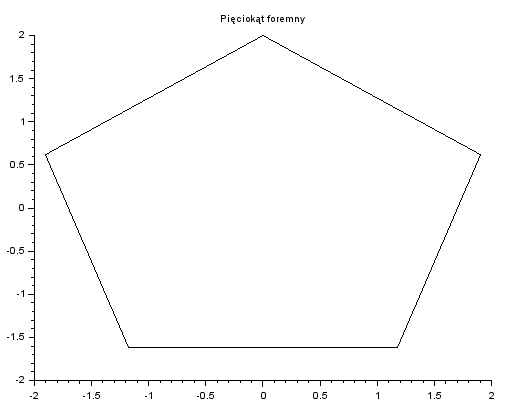
Narysujemy teraz łamaną, która ma tylko sześć punktów, szósty punkt jest identyczny z pierwszym.

t = linspace(0,2*%pi,6);
y = cos(t);
x = sin(t);
plot2d(x,y)
xtitle("Pięciokąt foremny") ⇒

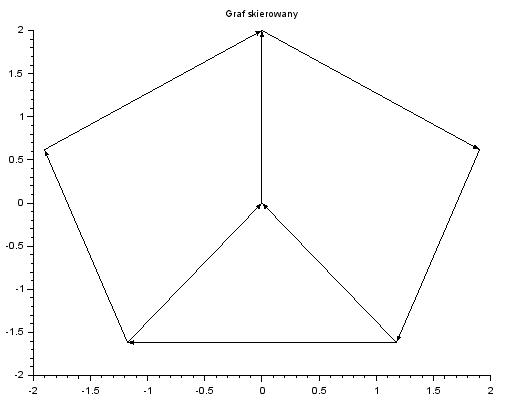
Do rysowania łamanych często wykorzystywane jest polecenie plot2d4(x,y), polecenie to, opisane wektorami $x$ i $y$ punkty łączy strzałkami. Wykorzystam wektory $t$, $x$ i $y$ z poprzedniego przykładu do narysowania grafu skierowanego.

plot2d4(x,y)
plot2d4([0 x(1)],[0 y(1)])
plot2d4([x(3) 0],[y(3) 0])
plot2d4([x(4) 0],[y(4) 0])
xtitle("Graf skierowany") ⇒

Wyrażenie x(n) oznacza n-tą współrzędną wektora $x$ – numeracja zaczyna się od 1. Wyrażenie x(p:k) oznacza podciąg wektora $x$ zaczynający się na miejscu $p$, a kończący na miejscu $k$.

a = 1:6 ⇒ 1.  2.  3.  4.  5.  6.
a(3)    ⇒ 3.
a(2:4)  ⇒ 2.  3.  4.

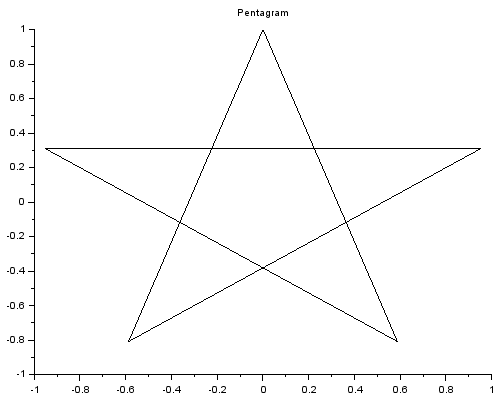
Narysuj pentagram. Pentagram można otrzymać z wierzchołków pięciokąta foremnego, łącząc co drugi wierzchołek.

Rozwiązanie

Podobieństwo pięciu instrukcji rysujących z powyższego zadania sugeruje, że życie byłoby prostsze gdybyśmy mieli do dyspozycji pętle.