Zadania można rozwiązać na wiele sposobów. Kliknięcie w przycisk
Rozwiązanie pozwala zobaczyć jeden z tych sposobów.
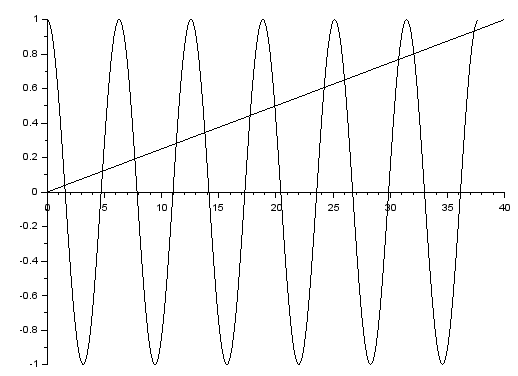
Poniżej - na jednym rysunku - znajdują się wykresy funkcji $y=cos(x)$ i $y=\frac{1}{40}\cdot x$. Znajdź dwa różne rozwiązania równania $$\frac{x}{40}=cos(x)$$.
Rozwiązanie
Musimy wybrać rozwiązywanie numeryczne. Kierując sie wykresem, wyznaczamy dwa przedziały $[a,b]$ oraz $[c,d]$ takie, że $f(a)\cdot f(b)\le 0$ oraz $f(c)\cdot f(d)\le 0$, gdzie
$f(x)=cos(x)-\frac{x}{40}$. Np.
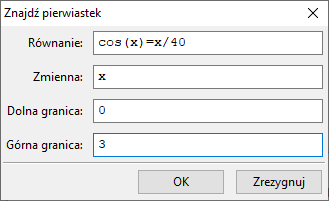
a = 0,
b = 3,
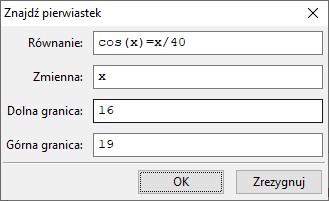
c = 16,
d = 19. Wykonujemy dwukrotnie polecenie
Równania ⇒ Znajdź pierwiastek:
Dostajemy rozwiązania $1.532475071451161$ i $17.7382096279117$.
Ukryj
Poniżej znajduje sie wykres funkcji $f(x)=e^{-x^2}$.
Czy $f(4)\lt 0,000001$?
Rozwiązanie
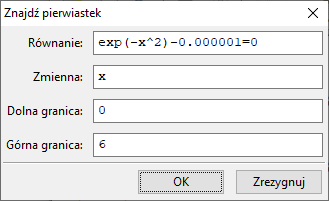
Niech $g(x)=f(x)-0,000001$. Poszukajmy rozwiązań równania $g(x)=0$ na przedziale $[0,6]$.
Rozwiązanie istnieje i jest równe $3.716922188849838\lt 4$. Funkcja $g$ jest dla $x\ge 0$ malejąca, zatem $g(4) \lt 0$ ⇒ $f(4)\lt 0,000001$.
Ukryj
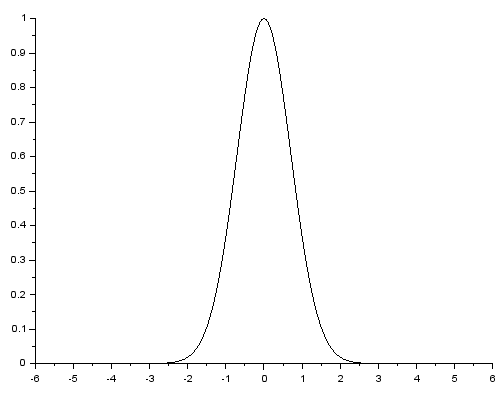Czy $f(4)\lt 0,000001$?
