Program Maxima

Możliwości pętli for znacznie wzrastają gdy korzystamy z tablic. Tablice w Maximie mogą być wielomiarowe, będziemy korzystać tylko z tablic dwuwymiarowych i jednowymiarowych. Warto pamiętać, że indeksowanie elementów w tablicy zaczyna sie od zera.

Tworzenie tablic.

• tablica jednowymiarowa array(nazwa,index_ostatniego_elementu),
• tablica dwuwymiarowa array(nazwa, index_ostatniego_wiersza, index_ostatniego_elementu_w_wierszu).

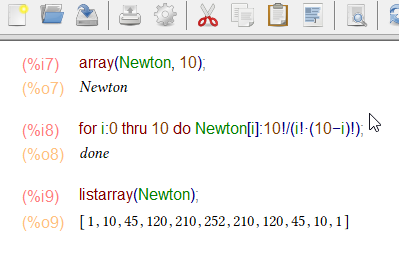
Tworzenie jednowymiarowej tablicy o nazwie Newton, zawierającej symbole Newtona $\binom{10}{0}\dots \binom{10}{10}$.

Obliczenie sumy liczb z tablicy Newton oraz wyznaczenie liczby największej i najmniejszej. Jeżeli w pętli for w kodzie po słowie do chcemy wykonać kilka instrukcji, to rozdzielamy je przecinkami i całość ograniczami nawiasami:

... do (instrukcja1,instrukcja2,...)

Utworzenie dwuwymiarowej tablicy o 2 wierszach i 21 kolumnach. Do pierwszego wiersza wpiszemy pierwsze 21 wyrazów ciągu Fibonacciego $f_0=1,\,f_1=1,\,f_n=f_{n-2}+f_{n-1}$ dla $n\ge 2$, w drugim wierszu na pozycji o indeksie $n$ ($n\gt 1$) wpiszemy $\frac{f_n}{f_{n-1}\cdot\phi}$ gdzie $\phi=\frac{1+\sqrt 5}{2}$ jest tzw. złotą liczbą.

array(fibo,1,20)
fibo[0,0]:1
fibo[0,1]:1
for i:2 thru 20 do 
fibo[0,i]:fibo[0,i-2]+fibo[0,i-1]
gold:(1+sqrt(5))/2
for i:1 thru 20 
do fibo[1,i]:fibo[0,i]/(fibo[0,i-1]*gold)
for i:0 thru 20 
do print(fibo[0,i],"  ",float(fibo[1,i]))

Ostatnie wiersze na ekranie wyglądają tak: