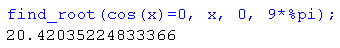Program Maxima

Maxima ma kilka poleceń do numerycznego rozwiązywania równań. Polecenia te znajdują się w pozycji Równania głównego menu.
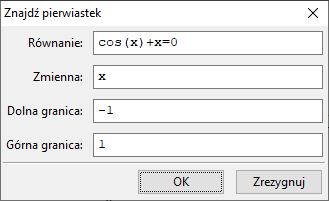
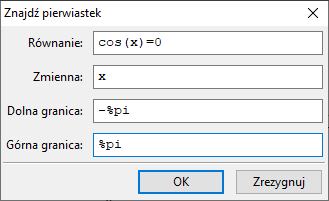
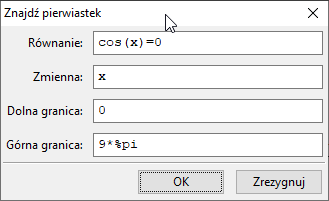
  • Znajdź pierwiastek, w otwierające się okienko wpisujemy równanie, symbol niewiadomej i końce przedziału, w którym szukamy rozwiązania.
    ⇒
    Uwagi
    Załózmy, że rozwiązujemy równanie postaci: $f(x)=0\,\,\,a\le x \le b$

    Maxima wykorzystuje metodę bisekcji, która wymaga by $f(a)\cdot f(b)\le 0$. W konsekwencji, Maxima odmawia współpracy, jeżeli $f(a)\cdot f(b) \gt 0$, również wtedy gdy w przedziale $[a,b]$ są rozwiązania równania.

    ⇒
    Jeżeli we wskazanym przedziale jest więcej rozwiązań, to Maxima znajduje tylko jedno z nich.
    ⇒
    Ukryj
  • Pierwiastki wielomianu, nie otwiera się okienko kreatora. Wielomian należy wpisać w głównym oknie programu wcześniej.
    ⇒
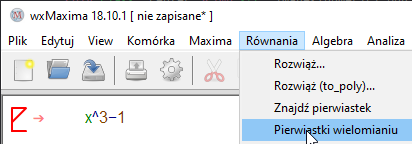    Wybrane polecenie znajduje wszystkie - również zespolone - pierwiastki wielomianu.
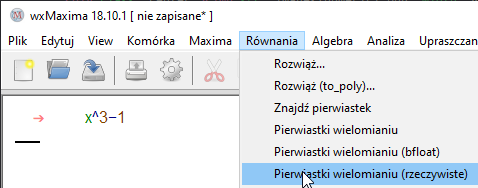
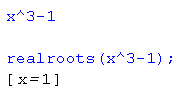
  • Pierwiastki wielomianu rzeczywiste, też nie otwiera się okna kreatora. Zgodnie z obietnicą, obliczane są tylko pierwiastki rzeczywiste.
    ⇒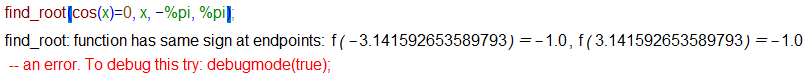