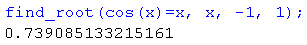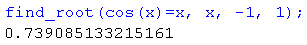Program Maxima
Równania można rozwiązywać dwoma sposobami:
- za pomocą przekształceń symbolicznych, przykłady to znane ze szkoły rozwiązywanie równań kwadratowych za pomocą wzorów Viete'a lub rozwiązywanie układów równań metodą podstawiania,
- numerycznie, podstawowe metody, to metoda bisekcji i metoda stycznych Newtona.
Każdy pakiet matematyczny potrafi rozwiązywać równania numerycznie. Maxima potrafi wykonywać przekształcenia symboliczne - mówimy, że Maxima ma własność CAS (Computer Algebra System).
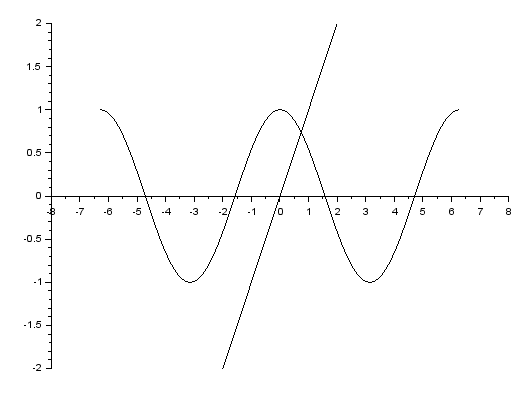
Metody numeryczne są uniwersalne, można nimi rozwiązać każde równanie, za pomocą przekształceń symbolicznych nie każde. Rozwiążmy równanie $cos(x)=x$. Z wykresu widać, że równanie ma rozwiązanie.
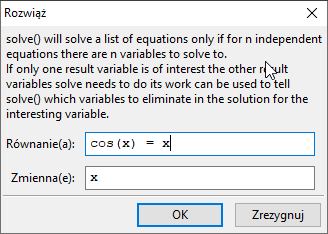
Rozwiązywanie symboliczne w Maximie Równania ⇒ Rozwiąż
daje mało przydatną odpowiedź:
Rozwiązywanie numeryczne Równania ⇒ Znajdź pierwiastek
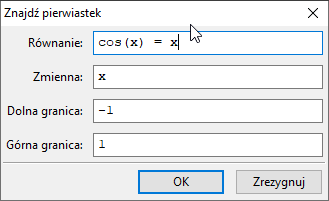wymaga co prawda podania przedziału, w którym szukamy rozwiązania, ale znajduje to rozwiązanie:
