LaTeX – bryły z prostopadłościanów

Rysowanie kostek z kształtami

Co to jest kształt

Kształtem jest polecenie LateX'a tworzące rysunek. Wypróbowałem następujące polecenia:

\pik (= \ensuremath {\spadesuit} 
\kier (= \ensuremath {\heartsuit} 
… 
\pgfimage {«nazwa_pliku»}

Dopuszczalne są na pewno pliki w formacie PNG i JPG, niedopuszczalne są formaty GIF i PS.

Plik graficzny musi się znajdować w katalogu z plikiem TEX. Nie trzeba wpisywać rozszerzenia. Jeśli w katalogu bieżącym są pliki Man.png i Man.jpg (lub Man.lpeg), to polecenie

\pgfimage {Man}

„wstawi” plik Man.png.

Wstęp

Do rysowania ścian kostki (równoległoboków z kształtami) wykorzystywane są przekształcenia afiniczne. W pakiecie TikZ przekształcenie afiniczne definiuje się tak:

\pgftransformcm {a} {c} {b} {d} {\pgfpoint {e} {f}}

Powyższe przekształcenie zapisane zapisane tradycyjnie wygląda tak: $A(x;\,y)=(ax+by+e;\,cx+dy+f)$, w szczególności $A(1;\,0)=(a;\,c)+(e;\,f),\,\,A(0;\,1)=(b;\,d)+(e'\,f)$.

Polecenie \pgfpoint wymaga podania jednostek.

Przykład:

\pgfpoint {2cm} {1cm}

Po zdefiniowaniu przekształcenia afinicznego $A$, polecenia

\draw figura;
\fill figura;

rysują $A(figura)$.

Po definicjach

\pgftransformcm {a} {c} {b} {d} {\pgfpoint {e} {f}} 
%przekszatłcenie A
… 
\pgftransformcm {g} {h} {i} {j} {\pgfpoint {k} {l}} 
%przekszatłcenie B

pakiet TikZ korzysta ze złożenia $A\cdot B$. Na ogół jest to niepożądane, warto każde polecenie pgfrtansformcm poprzedzić poleceniem pgftransformreset.

Definicje przekształceń afinicznych są „lokalne” – przekształcenie zdefiniowane w otoczeniu tikzpicture nie jest stosowane w kolejnych otoczeniach tikzpicture.

\shapes (\unroundedshapes)

Prostopadłościan opisany na kostce wygląda tak:

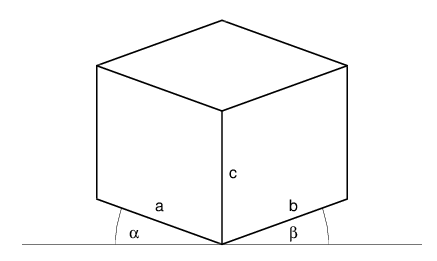
Wartości domyślne są następujące:

c = 3
leftScale = 1.0
rightScale = 1.0
a = leftScale*c
b = rightScale*c
α = 20°
β = 20°

Do zmiany wartości domyślnych służą polecenia:

\edef\size {nowa_wartość_c}
\computeLeft {nowa_wartość_α} {nowa_wartość_leftScale}
\computeRight {nowa_wartość_β} {nowa_wartość_rightScale}

Makrodefinicja shapes korzysta z makrodefinicji face, a makrodefinicja unroundedshapes z makrodefinicji unroundedfave.

Makrodefinicje shapes i unroundeddshapes rysują kostkę skierowaną krawędzią do przodu. Mają pięć argumentów:

pierwsze dwa to współrzędne najniższego punktu
trzeci ma postać:
```
 {kształt₁/kolor₁, kształt₂/kolor₂, kształt₃/kolor₃}
```
kolejne wyrazy opisują kształt rysowany na ścianie i kolor wypełnienia, kolejność: prawa ściana, lewa ściana, górna ściana
czwarty parametr to współczynnik skalowania obramowań
piąty parametr to współczynnik skalowania kształtu

Przykłady:

\shapes {0} {0} { {\pik/red!20!white, \karo/blue!20!white, \kier/green!20!white}} {2} {3}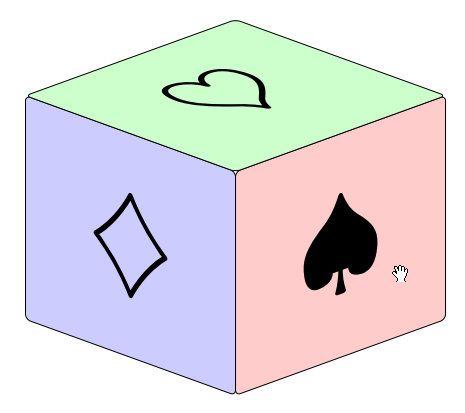

⇒

\unroundedshapes {0} {0} { {\kier/yellow, \kier/green!20!white, \pik/yellow}} {1} {1}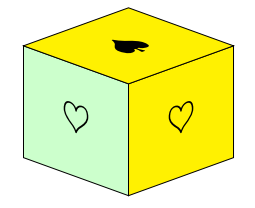

⇒

\frontshapes (\unroundedfrontshapes)

Prostopadłościan opisany na kostce wygląda tak:

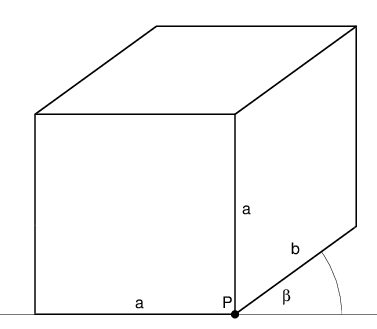
Wartości domyślne są następujące:

a = 3
frontScale = 0.75
b = frontScale*a
β = 36°

Do zmiany wartości domyślnych służą polecenia:

\edef\size {nowa_wartość_a}
\computeFront {nowa_wartość_β} {nowa_wartość_frontScale}

Makrodefinicja frontshapes korzysta z makrodefinicji face, a makrodefinicja unroundedfrontshapes z makrodefinicji unroundedface.

Makrodefinicje frontshapes i unroundedfrontshapes rysują kostkę skierowaną ścianą do przodu. Mają pięć argumentów:

pierwsze dwa to współrzędne najniższego punktu
trzeci ma postać:
```
 {kształt₁/kolor₁, kształt₂/kolor₂, kształt₃/kolor₃}
```
kolejne wyrazy opisują kształt rysowany na ścianie i kolor wypełnienia, kolejność: prawa ściana, lewa ściana, górna ściana
czwarty parametr to współczynnik skalowania obramowań
piąty parametr to współczynnik skalowania kształtu

Przykłady:

\frontshapes {3} {0} { {\pik/green!20!white, \trefl/blue!20!white, \karo/green!20!white}} {2} {2}}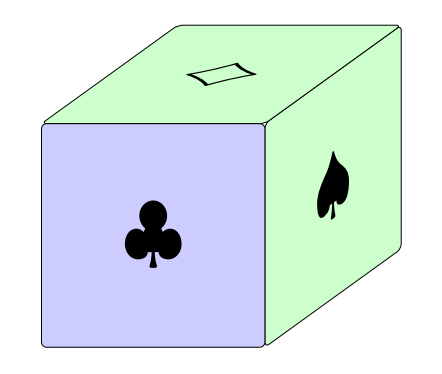

⇒

\unroundedfrontshapes {0} {0} { {\pik/green!20!white, \trefl/blue!20!white, \pik/green!20!white}} {1.5} {1}
\unroundedfrontshapes {4} {0} { {\pik/white, \trefl/blue!20!white, \pik/white}} {1.5} {1.5}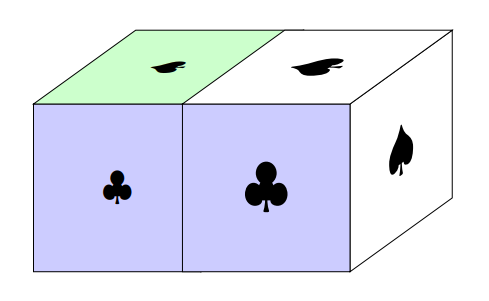

⇒

\face (\unroundedface)

Makrodefinicja face rysuje zaokrąglony kwadrat jednostkowy z kształtem. Ma pięć argumentów:

pierwszy to kształt
drugi to kolor wypełnienia kwadratu – krawędzie są czarne
trzeci decyduje czy narysowany zostanie kształt, czy jego odbicie symetryczne względem osi $Oy$
czwarty to współczynnik skalowania kwadratu
piąty to współczynnik skalowania kształtu

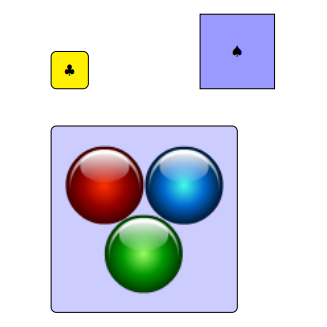
Makrodefinicja unroundedface różni się od face tylko tym, że rysuje „niezaokrąglony” kwadrat. Przykład:

\face {\trefl} {yellow} {1} {1} {1}
\pgftransformreset 
\pgftransformcm {1} {0} {0} {1} {\pgfpoint {4cm} {0cm}} 
\unroundedface {\pik} {blue!40!white} {1} {2} {1} 
\pgftransformreset
\pgftransformcm {1} {0} {0} {1} {\pgfpoint {0cm} {-6cm}}
\face {\pgfimage {Colors_128}} {blue!20!white} {-1} {5} {1}