LaTeX – bryły z prostopadłościanów

Rysowanie brył

Bryły budowane są z takich prostopadłościanów:

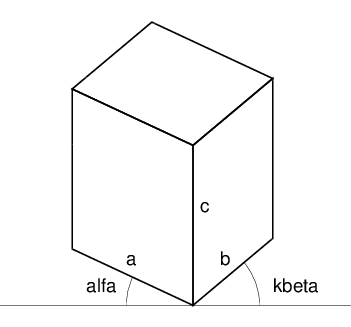
Domyślnie, tzn. po wykonaniu polecenia

\input{edge}

wartości wymiarów prostopadłościanów są następujące:

a = 1
b = 0.65
c = 1.2
alfa = 25°
kbeta = 40°

Można te wymiary zmieniać (w preambule lub w sekcji document), np. tak:

\edef\b{0.8}

Po zmianie tych wymiarów konieczne jest obliczenie kilku pomocniczych wielkości. Można to zrobić poleceniem:

\update

Wspomniane obliczenie jest konieczne tylko przed poleceniami wall, pyramid, otherwall i otherpyramid
Kolory ścian i kolor krawędzi dla makrodefinicji contour ustala się argumentami makrodefinicji. Kolor krawędzi dla pozostałych makrodefinicji można zmienić tak:

\edef\linecolor{<nazwa_koloru>}

Domyślnie jest to kolor czarny (black).
Uwaga W opisie funkcji często używam zwrotu najniższy punkt. Punkt ten jest rzeczywiście najniższy gdy kąty alfa i kbeta są dodatnie. Gdy jeden z kątów jest równy zero a drugi jest dodatni, to wspomniany punkt jest jednym z najniżej położonych punktów. Domyślności czytającego pozostawiam ustalenie którym konkretnie. Jeśli co najmniej jeden z kątów alfa, kbeta jest ujemny, wspomniany punkt nie jest najniższy,

cube

Makrodefinicja cube ma pięć argumentów. Pierwsze dwa argumenty to współrzędne najniższego punktu, kolejne trzy to kolory ścian: górnej, prawej i lewej.

\cube{2}{2}{green}{blue!40!white}{red}
\edef\linecolor{white}
\cube{4}{2}{blue!10!white}{blue!40!white}{blue!10!white}
\edef\alfa{0}
\cube{6}{2}{green}{blue!40!white}{red}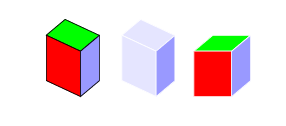

⇒

tower

Makrodefinicja tower ma siedem argumentów. Pierwsze dwa argumenty to współrzędne najniższego punktu, trzeci argument to wysokość wieży (w prostopadłościanach), kolejne trzy to kolory ścian: górnej, prawej i lewej. Siódmy argument to liczba „pustych” prostopadłościanów na dole wieży.

\tower{2}{2}{3}{blue!10!white}{blue!40!white}{blue!10!white}{0}
\tower{4}{2}{3}{blue!10!white}{blue!40!white}{blue!10!white}{0}
\tower{4}{2}{2}{green}{blue!40!white}{red}{3}
\edef\kbeta{0}
\tower{6}{2}{3}{blue!10!white}{blue!40!white}{blue!10!white}{1}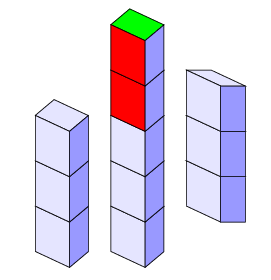

⇒

othertower

Makrodefinicja othertower ma sześć argumentów. Pierwsze dwa argumenty to współrzędne najniższego punktu, trzeci argument to ciąg liczb – wysokości (w prostopadłościanach) na których znajdują się kostki tworzące wieżę, kolejne trzy to kolory ścian: górnej, prawej i lewej.

\othertower{2}{2}{{1, 3, 5}}{blue!40!white}{blue!10!white}{blue!10!white}
\othertower{4}{2}{{0, 2, 4}}{blue!40!white}{blue!10!white}{blue!10!white}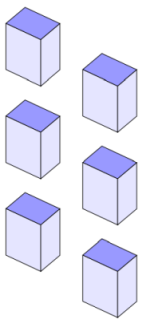

⇒

wall

Makrodefinicja wall ma sześć argumentów. Pierwsze dwa argumenty to współrzędne najniższego punktu, trzeci argument opisuje wieże (tower) – od lewej do prawej – tworzące mur, kolejne trzy to kolory ścian: górnej, prawej i lewej.
Postać trzeciego argumentu:

{w₁/l₁,w₂/l₂,…,w_n/l_n}

$n$ jest liczbą wież, wyrażenie $w_i/l_i$ opisuje $i$-tą (licząc od lewej) wieżę: $w_i$ jest wysokością wieży (w prostopadłościanach), $l_i$ jest liczbą „pustych” prostopadłościanów na dole wieży.

\wall{2}{2}{{3/0,2/0,3/1}}{blue!10!white}{blue!40!white}{blue!10!white}
\wall{6}{2}{{2/1,2/0,3/1}}{blue!10!white}{green!40!white}{green!10!white}
\edef\kbeta{10}
\update
\wall{10}{2}{{2/1,2/0,3/1}}{blue!10!white}{green!40!white}{green!10!white}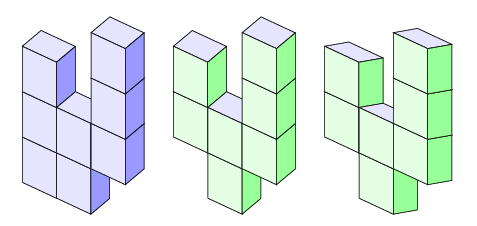

⇒

otherwall

Makrodefinicja otherwall ma sześć argumentów. Pierwsze dwa argumenty to współrzędne najniższego punktu, trzeci argument opisuje wieże (othertower) – od lewej do prawej – tworzące mur, kolejne trzy to kolory ścian: górnej, prawej i lewej.
Postać trzeciego argumentu:

(w₁,w₂,…,w_n)

$n$ jest liczbą wież, wyrażenie $w_i$ opisuje $i$-tą (licząc od lewej) wieżę.

\otherwall{2}{2}{{{1,3,5},{0,1,2,3}}}{blue!10!white}{blue!40!white}{blue!10!white}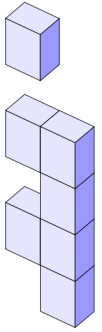

⇒

pyramid

Makrodefinicja pyramid ma sześć argumentów. Pierwsze dwa argumenty to współrzędne najniższego punktu, trzeci argument opisuje prawe mury (wall) tworzące piramidę – na poniższym rysunku prawe są mury z czerwoną boczną ścianą, kolejne trzy to kolory ścian: górnej, prawej i lewej.

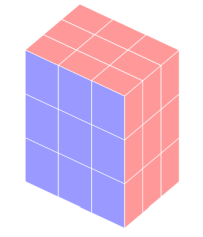
Postać trzeciego argumentu:

{mur₁,mur₂,…,mur_n}

$n$ jest liczbą murów, wyrażenie $\text{mur}_i$ opisuje $i$-ty (licząc od tyłu) mur.

\edef\linecolor{red}
\pyramid{2}{2}{{3/0,3/0,2/0},{3/0,1/0,3/0},{1/0,3/0,1/1}}{blue!40!white}{blue!10!white}{blue!10!white}
\contour{2}{2}{3}{3}{3}{green}
\pyramid{7}{2}{{3/0},{3/0}}{blue!40!white}{blue!10!white}{blue!10!white}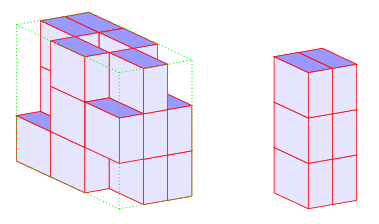

⇒

otherpyramid

Makrodefinicja otherpyramid ma sześć argumentów. Pierwsze dwa argumenty to współrzędne najniższego punktu, trzeci argument opisuje prawe mury (wall) tworzące piramidę – na poniższym rysunku prawe są mury z czerwoną boczną ścianą, kolejne trzy to kolory ścian: górnej, prawej i lewej.

Postać trzeciego argumentu:

{mur₁,mur₂,…,mur_n}

$n$ jest liczbą murów, wyrażenie $\text{mur}_i$ opisuje $i$-ty (licząc od tyłu) mur.

\otherpyramid{2}{2}{{{1,3,4},{0,1,2,3}},{{1,3,4},{0,1,2,3}},{{1,3,4},{1,2}}}{blue!10!white}{blue!40!white}{blue!10!white}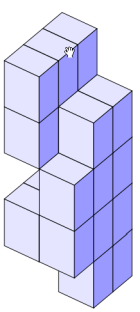

⇒

contour

Makrodefinicja contour rysuje – linią przerywaną o szerokości 0,2mm – krawędzie prostopadłościanu. Ma ona sześć argumentów. Pierwsze dwa argumenty to współrzędne najniższego punktu, kolejne trzy to wymiary prostopadłościanu, wymiary podajemy jako wielokrotności $a,\,b,\,c$. Szósty argument to kolor.

\contour{2}{2}{4}{3}{2}{red}
\contour{7}{2}{1}{1}{1}{red}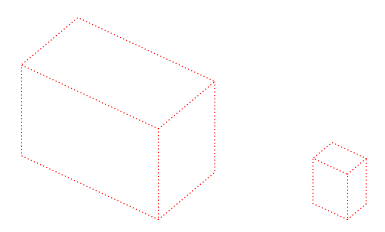

⇒

rightside

Makrodefinicja rightside ma trzy argumenty. Pierwsze dwa argumenty to współrzędne najniższego punktu, trzeci argument to kolor.

\rightside{2}{2}{red!50!white}
\edef\kbeta{60}
\edef\b{1}
\rightside{4}{3}{red!50!blue}
\edef\kbeta{-60}
\rightside{6}{3}{red!50!blue}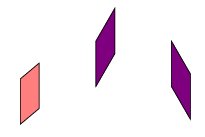

⇒

leftside

Makrodefinicja leftside ma trzy argumenty. Pierwsze dwa argumenty to współrzędne najniższego punktu, trzeci argument to kolor.

\leftside{2}{2}{red!50!white}
\edef\alfa{45}
\edef\c{2}
\leftside{4}{3}{red!50!green}
\edef\alfa{-45}
\leftside{6}{3}{red!50!blue}}

⇒

topside

Makrodefinicja topside ma trzy argumenty. Pierwsze dwa argumenty to współrzędne najniższego punktu, trzeci argument to kolor.

\edef\a{2}
\edef\b{2}
\topside{2}{2}{red!50!white}
\edef\alfa{40}
\edef\kbeta{25}
\topside{6}{2}{red!50!green}

⇒