Fraktale
Znaczenie terminu fraktal nie jest ściśle określone. Na tej stronie słowo fraktal oznaczać będzie zbiór
(zazwyczaj podzbiór $\mathbb{R}^2$) o matematycznie prostej definicji oraz skomplikowanym i fascynującym wyglądzie. Według powyższej definicji fraktal jest zbiorem, zatem rysunek fraktala winien
być dwukolorowy (czarno-biały): albo punkt należy do zbioru, albo nie. Atrakcyjność rysunku można zwiększyć przez pokolorowanie – punkty należące do zbioru rysowane są zazwyczaj kolorem
czarnym, kolor punktów nie należących do zbioru jest wyznaczany przez pewną regułę matematyczną.
Wszystkie rysunki na tej stronie wykonywane są w naturalnej dla matematyków orientacji – współrzędna $y$ rośnie do góry. W większości języków programowania współrzędna $y$ rośnie w dół, w konsekwencji wiele rysunków fraktali, które można znaleźć w internecie jest odbiciem symetrycznym rysunków z tej strony.
Zbiór Mandelbrota
Benoit Mandelbrot miał (5 i 6 maja 2005 roku) wykłady na Wydziale Matematyki i Informatyki w Poznaniu. Tematy wykładów:
- Beauty and the beast: From the study of rough shapes to the mathematical magic of fractals
- The unity of mathematics: from the „Fundamenta” to the fractal geometry of roughness
 |
Dla każdej liczby zespolonej $c$ definiujemy funcję $f_c:\mathbb{C} \rightarrow \mathbb{C}$ wzorem: $f_c(z) = z^2 + c$. Liczba $c$ należy do zbioru Mandelbrota wtedy i tylko wtedy gdy orbita liczby $0$ dla funkcji $f_c$ jest ograniczona. Równoważna definicja: liczba zespolona $c$ należy do zbioru Mandelbrota wtedy i tylko wtedy gdy zbiór Julli $J_c$ jest spójny. Równoważność tych definicji jest dość trudna do udowodnienia. Analogicznie – ograniczając się do liczb rzeczywistych $c$ – można zdefiniować rzeczywisty zbiór Mandelbrota (podzbiór $\mathbb{R}$). Rzeczywisty zbiór Mandelbrota jest przekrojem zespolonego zbioru Mandelbrota i osi rzeczywistej. W rzeczywistym zbiorze Mandelbrota nie ma nic ciekawego, jest on przedziałem $[-2;\, 0,25]$ (punkt 4). Można łatwo wykazać (punkt 2), że jeśli $|c| \gt 2$, to ciąg $(z_n)$ jest nieograniczony. Wynika stąd, że zbiór Mandelbrota jest podzbiorem koła o środku $0$ i promieniu $2$. Łatwo z tego wywnioskować (punkt 3), że jeśli dla pewnego $n$ zachodzi nierówność: $|z_n| \gt 2$, to liczba $c$ nie należy do zbioru Mandelbrota. |
Powyższa własność sugeruje następujący algorytm rozstrzygania, które liczby zespolone $c$ należy do do zbioru Mandelbrota:
- ustalamy liczbę naturalną $N$ (= liczba iteracji)
- obliczamy $N$ pierwszych wyrazów ciągu ($z_n)_{n \ge 0}\,\, (z_0 = 0$)
- jeśli dla pewnego $n\,\, |z_n| \gt 2$, to liczba $c$ nie należy do zbioru Mandelbrota – decyzja taka jest zawsze poprawna
- jeśli dla wszystkich $n \le \mathbb{N}\,\, |z_n| \lt 2$, to liczba $c$ należy do zbioru Mandelbrota – niezależnie od tego jak duże jest $N$ decyzja taka będzie błędna dla pewnych liczb $c$.
Jeżeli $c = 0,25 + a$ ($a \gt 0$), to (punkt 4) ciąg $(z_n)_{n \ge 0}$ jest rosnący i nieograniczony.
Oznaczmy symbolem $\phi(a)$ najmniejszą liczbę naturalną $n$ taką, że $|z_n| \gt 2$.
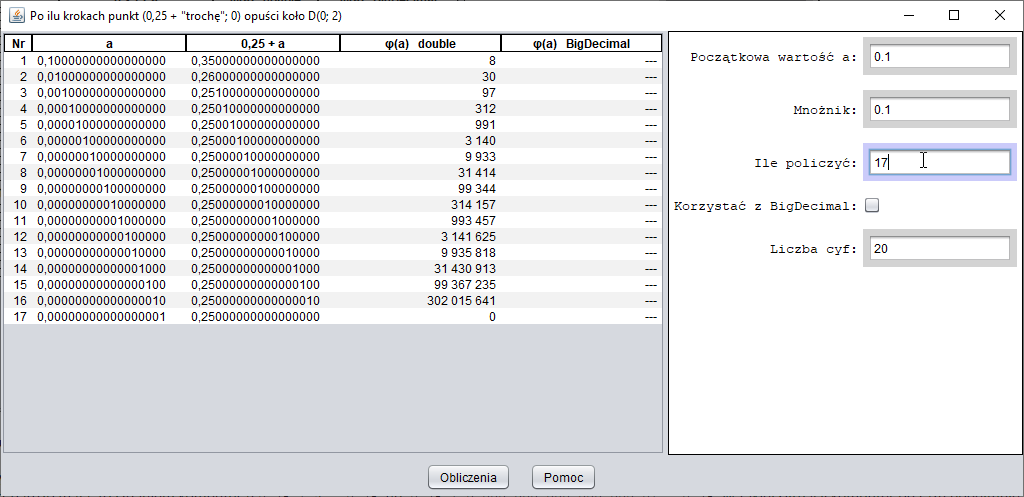
Plik FunctionPhi.zip zawiera program obliczający wartości funkcji $\phi$.
- Dlaczego w powyższej tabeli pojawia się wartość $0$?
Jeżeli liczba $a$ jest bardzo mała, to (zdaniem komputera) $0,25 + a = 0,25$, np. $0,25 + 0,000\, 000\, 000\, 000\, 000\, 01 = 0,25$. W takiej sytuacji komputer od razu podejmuje decyzję, że orbita liczby $0,25 + a = 0,25$ jest ograniczona. - Czy pojawienie sie liczby $0$ podważa sensowność algorytmu?
Nie: załóżmy że obszar przeznaczony na rysunek ma szerokość 401 pikseli. Badamy tylko takie liczby zespolone $c$, że $-2 \le \Re(c) \le 2$. Zatem dla każdej badanej liczby $c,\,\, \Re(c) = -2 + k\cdot 0,01,\,\, 0 \le k \le 400$ ⇒ najmniejsza badana wartość $a$ wynosi $0,01$.

Płonący statek
Artykuł w Wikipedii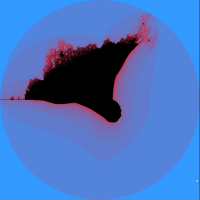 |
Efektowny rysunek „płonącego statku” można obejrzeć w Wikipedii. Niech funkcja $g:\mathbb{C} \rightarrow \mathbb{C}$ będzie określona wzorem: $g(z) = g(x+y\cdot\imath) = |x| + |y|\cdot\imath$. Dla każdej liczby zespolonej $c$ definiujemy funkcję $h_c:\mathbb{C} \rightarrow \mathbb{C}$ wzorem: $h_c(z) = g(z)^2 + c$. Liczba $c$ należy do zbioru o nazwie Burning Ship wtedy i tylko wtedy gdy orbita liczby $0$ dla funkcji $h_c$ jest ograniczona. Analogicznie – ograniczając się do liczb rzeczywistych $c$ – można zdefiniować rzeczywisty „płonący statek”. Ponieważ dla liczb rzeczywistych $z,\, c$ zachodzi równość $h_c(z) = f_c$, to rzeczywisty „płonący statek” jest identyczny z rzeczywistym zbiorem Mandelbrota. Analogicznie jak dla zbioru Mandelbrota można wykazać, że płonący statek jest podzbiorem koła o środku $0$ i promieniu $2$. |
Plik BurningShip.zip zawiera program rysujący zbiór Burning Ship.

Zbiory Julii
Kim był Gaston Julia.
$c = -0,1 + 0,65\dot i$ |
Niech $c$ oznacza liczbę zespoloną. Definiujemy funkcję $f_c:\mathbb{C} \rightarrow \mathbb{C}$ wzorem: $f_c=z^2 + c$. Mówimy, że liczba zespolona $z$ jest więźniem odwzorowania $f_c$ gdy jej
orbita dla funkcji $f_c$ jest ograniczona. Zbiór więźniów oznaczmy symbolem $W_c$. Zbiorem Julii $J_c$ odwzorowania $f_c$ nazywamy brzeg zbioru $W_c$. Znaczenie zwrotu Można wykazać (punkt 5), że zbiór więźniów $W_c$ (a w konsekwencji zbiór Julii $J_c$) jest podzbiorem koła o środku $0$ i promieniu $\max(2,|c|)$. Można też wykazać, że zachodzi alternatywa: zbiór Julii $J_c$ jest albo spójny albo całkowicie niespójny. Tradycyjnie mówi się o rysowaniu zbiorów Julii, chociaż naprawdę rysowane są zbiory więźniów $W_c$. Ograniczając się do liczb rzeczywistych $c$ można zdefiniować rzeczywiste zbiory Julii (podzbiory $\mathbb{R}$). Rzeczywiste zbiory Julii są przekrojami zespolonych zbiorów Julii i osi rzeczywistej. W wyglądzie rzeczywistych
zbiorów Julii nie ma niczego fascynującego: jeśli $c \gt \frac{1}{4}$, to zbiór $W_c$ jest pusty (punkt 6),
|

Zasady kolorowania
Wszystkie programy pozwalają wykonać rysunek kolorowy i czarno-biały. W obu wersjach rysunku punkty należące do fraktala (więźniowie) są czarne. W wersji czarno-białej, punkty nie należące do fraktala (uciekinierzy) są białe.
Niech $n$ oznacza liczbę iteracji, tzn. liczbę obliczanych wyrazów ciągu, a $k \le n$ niech oznacza numer wyrazu w ciągu po obliczeniu którego, podejmujemy decyzję, że punkt płaszczyzny jest uciekinierem – nie należy do fraktala.
W wersji kolorowej, do wyboru koloru stosowany jest jeden z dwóch algorytmów:
- ustalamy listę kolorów $\text{kol}_0,\text{kol}_1,\ldots,\text{kol}_{m-1}$, kolor uciekiniera to $\text{kol}_{k\%m}$
($k\%m$ oznacza resztę z dzielenia $k$ przez $m$, liczba iteracji $n$ nie ma wpływu na kolor)
Domyślna lista kolorów wygląda tak:- #001199
- #ffcc33
- #c0c0c0
- #33cc00
- #cc0000
- #006666
- ustalamy dwa kolory $\text{kol}_0$ i $\text{kol}_1$, dla uciekiniera obliczamy współczynnik $w$: $w = \sqrt[4]{\frac{k}{n}}$ dla zbioru Mandelbrota, $w = \sqrt{\frac{k}{n}}$ dla zbiorów Julii i płonącego statku,
oczywiście $0 \le w \le 1$
przy ustaleniu koloru korzystamy z modelu RGB, składowa czerwona koloru uciekiniera to: $w\cdot \text{kol}_0\cdot \text{red} + (1-w)\cdot \text{kol}_1\cdot \text{red}$ ($\text{red}$ oznacza składową czerwoną koloru), analogiczne wzory są stosowane do składowych $\text{blue}$ i $\text{green}$. Kolory domyślne dla zbioru Burning Ship:- #fd9900
- #3300ff
- #fd9900
- #009900
Przydatne pojęcia matematyczne
- Zbiór $A$ jest spójny, jeżeli każdy jego domknięty podzbiór $E$ spełnia warunek: $(E = \emptyset) \lor (E = A)$. Matematyczne pojęcie zbioru spójnego odpowiada potocznemu pojęciu zbioru jednokawałkowego.
- Zbiór $A$ jest całkowicie niespójny, jeżeli każdy jego spójny podzbiór jest jednopunktowy.
- Niech $f:\mathbb{C} \rightarrow \mathbb{C}$ będzie ustaloną funkcją. Dla każdej liczby zespolonej $w$ określony rekurencyjnie ciąg liczb zespolonych: $z_0=w,\, z_1=f(z_0),\ldots,z_{n+1}=f(z_n)$ nazywamy orbitą liczby $w$.
- Więźniowie i uciekinierzy. Dla każdej funkcji $f:\mathbb{C} \rightarrow \mathbb{C}$ liczbę zespoloną $w$ nazywamy więźniem (dla funkcji $f$) jeśli orbita liczby $w$ jest ograniczona, liczbę zespoloną, która nie jest więźniem nazywamy uciekinierem. Zbiór więźniów funkcji $f$ oznaczamy $W_f$, a zbiór uciekinierów $U_f$. Pojęcie więźnia i uciekiniera można stosować w sytuacji ogólniejszej: $f:X \rightarrow X$, gdzie $X$ jest dowolną przestrzenią, w której ma sens pojęcie ograniczoności ($\mathbb{R}$, $\mathbb{R}^3$).
Uruchamianie programów
Programy napisane są w Javie, do ich uruchomienia niezbędne jest zainstalowanie JRE (wersja ≥ 8), JRE można pobrać stąd.
Linki na stronie prowadzą do plików zip. Ściągnięty plik zip należy rozpakować (w dowolnym katalogu), zawiera on plik jar oraz katalog resources z ikonami i opisem programu (format HTML).
W systemie Windows program można uruchomić podwójnym kliknięciem w plik jar.
Lista programów: