Rysowanie kości do gry

Do rysowania ścian kostki (równoległoboków z kropkami) wykorzystywane są przekształcenia afiniczne. W pakiecie TikZ przekształcenie afiniczne definiuje się tak:

\pgftransformcm{a}{c}{b}{d}{\pgfpoint{e}{f}}

Powyższe przekształcenie zapisane zapisane tradycyjnie wygląda tak: $A(x,y)=(ax+by+e,cx+dy+f)$, w szczególności $A(1,0)=(a,c)+(e,f),\,\,A(0,1)=(b,d)+(e,f)$.

Polecenie \pgfpoint wymaga podania jednostek.

Przykład:

\pgfpoint{2cm}{1cm}

Po zdefiniowaniu przekształcenia afinicznego $A$, polecenia

\draw figura
\fill figura

rysują $A(figura)$.

Po definicjach

\pgftransformcm{a}{c}{b}{d}{\pgfpoint{e}{f}} – przekszatłcenie A
…
\pgftransformcm{g}{h}{i}{j}{\pgfpoint{k}{l}} – przekszatłcenie B

pakiet TikZ korzysta ze złożenia $A\cdot B$. Na ogół jest to niepożądane, warto każde polecenie pgfrtansformcm poprzedzać poleceniem pgftransformreset.

Definicje przekształceń afinicznych są „lokalne” – przekształcenie zdefiniowane w otoczeniu tikzpicture nie jest stosowane w kolejnych otoczeniach tikzpicture.

dice (unroundeddice)

Prostopadłościan opisany na kostce wygląda tak:

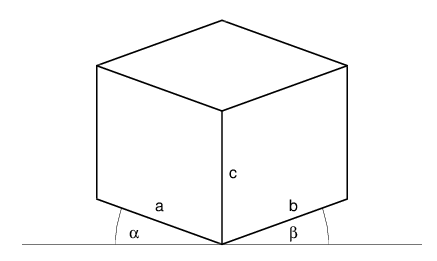
Wartości domyślne są następujące:

c = 3
leftScale = 1.0
rightScale = 1.0
a = leftScale⋅c
b = rightScale⋅c
α = 20°
β = 20°

Do zmiany wartości domyślnych służą polecenia:

\edef\size{nowa_wartość_c}
\computeLeft{nowa_wartość_α}{nowa_wartość_leftScale}
\computeRight{nowa_wartość_β}{nowa_wartość_rightScale}

Makrodefinicja dice korzysta z makrodefinicji face, a makrodefinicja unroundeddice z makrodefinicji unroundedface.

Makrodefinicje dice i unroundeddice rysują kostkę skierowaną krawędzią do przodu. Mają cztery argumenty:

pierwsze dwa to współrzędne najniższego punktu
trzeci ma postać:
```
{liczba₁/kolor₁, liczba₂/kolor₂, liczba₃/kolor₃}
```
kolejne wyrazy opisują liczbę kropek na ścianie i kolor tła, kolejność: prawa ściana, lewa ściana, górna ściana – krawędzie są czarne
czwarty parametr to kolor kropek

Przykład:

\dice{3}{0}{{4/red, 5/red ,2/red}}{white}
\edef\size{2}
\dice{6}{0}{{4/red, 5/red ,2/red}}{white}  ⇒

Lewa kostka ma domyślną długość krawędzi ($3$), polecenie

\edef\size{2}

zmieniło długość krawędzi na $2$.

frontdice (unroundedfrontdice)

Prostopadłościan opisany na kostce wygląda tak:

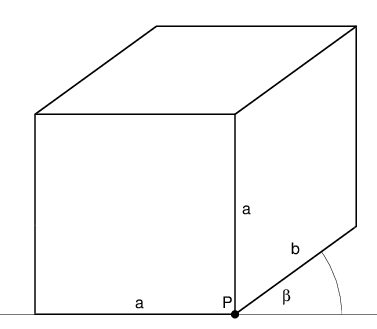
Wartości domyślne są następujące:

a = 3
frontScale = 0.75
b = frontScale*a
β = 36°

Do zmiany wartości domyślnych służą polecenia:

\edef\size{nowa_wartość_a}
\computeFront{nowa_wartość_β}{nowa_wartość_frontScale}

Makrodefinicja frontdice korzysta z makrodefinicji face, a makrodefinicja unroundedfrontdice z makrodefinicji unroundedface.

Makrodefinicje frontdice i unroundedfrontdice rysują kostkę skierowaną ścianą do przodu. Mają cztery argumenty:

pierwsze dwa to współrzędne najniższego punktu
trzeci ma postać:
```
{liczba₁/kolor₁, liczba₂/kolor₂, liczba₃/kolor₃}
```
kolejne wyrazy opisują liczbę kropek na ścianie i kolor tła, kolejność: prawa ściana, lewa ściana, górna ściana – krawędzie są czarne
czwarty parametr to kolor kropek

Przykład:

\frontdice{3}{0}{{4/red, 5/red, 2/red}}{white}
\frontdice{6}{0}{{4/red, 5/red, 2/red}}{white}  ⇒

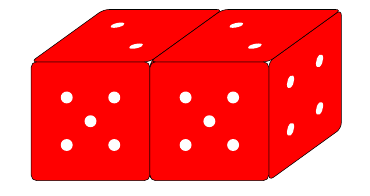
face (unroundedface)

Makrodefinicja face rysuje zaokrąglony kwadrat jednostkowy z kropkami. Ma trzy argumenty: pierwszy to kolor kropek, drugi to kolor wypełnienia kwadratu – krawędzie są czarne, trzeci to liczba kropek (musi być z zakresu $1-6$).

\face{white!50!red}{red}{6}
\pgftransformreset
\pgftransformcm{0.71*3}{0.71*3}{-0.71*3}{0.71*3}{\pgfpoint{3cm}{0cm}}
\face{white!50!red}{red}{6}  ⇒

Makrodefinicja unroundedface różni się od face tylko tym że rysuje „niezaokrąglony” kwadrat.

\unroundedface{white!50!red}{red}{6}
\pgftransformreset
\pgftransformcm{0.71*3}{0.71*3}{-0.71*3}{0.71*3}{\pgfpoint{3cm}{0cm}}
\unroundedface{white!50!red}{red}{6}  ⇒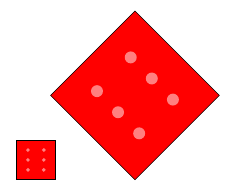

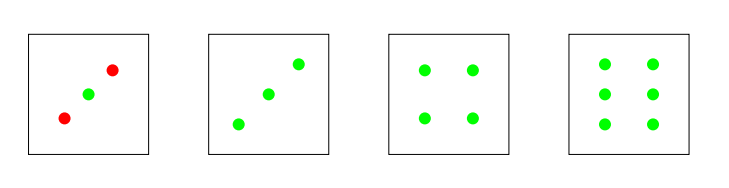
onedot, twodots, threedots, fourdots, sixdots

Każda z tych makrodefinicji rysuje pewną liczbę kropek (kółek o promieniu $0.05$). Wszystkie mają jeden argument: kolor kropki.

Polecenie	Współrzędne środków kropek
onedot	$(0,5;\, 0,5)$
twodots	$(0,3;\, 0,3),\, (0,7;\, 0,7)$
threedots	$(0,25;\, 0,25),\, (0,5;\, 0,5),\, (0,75;\, 0,75)$
fourdots	$(0,3;\, 0,3),\, (0,3;\, 0,7),\, (0,7;\, 0,3),\, (0,7;\, 0,7)$
sixdots	$(0,3;\, 0,25),\, (0,3;\, 0,5),\, (0,3;\, 0,75),\, (0,7;\, 0,25),\, (0,7;\, 0,5),\, (0,7;\, 0,75)$

Polecenia rysującego pięć kropek nie ma. Pięć kropek jest rysowanych sekwencją poleceń: onedot i fourdots.

\pgftransformreset
\pgftransformcm{2}{0}{0}{2}{\pgfpoint{0}{0}}
\draw rectangle(1,1);
\onedot{green}
\twodots{red}
\pgftransformcm{1}{0}{0}{1}{\pgfpoint{1.5cm}{0}}
\draw rectangle(1,1);
\threedots{green}
\pgftransformcm{1}{0}{0}{1}{\pgfpoint{1.5cm}{0}}
\draw rectangle(1,1);
\fourdots{green}
\pgftransformcm{1}{0}{0}{1}{\pgfpoint{1.5cm}{0}}
\draw rectangle(1,1);
\sixdots{green}  ⇒