Arkusze kalkulacyjne Excel i Calc
Równania
Arkusze są wyposażone w narzędzie nazywające się Szukaj wyniku, potrafiące rozwiązać dowolne równanie z jedną niewiadomą.
Równania $e^{x^2}-1=\cos x$ nie potrafimy rozwiązać, a z wykresu widać, że to równanie ma dwa rozwiązania.
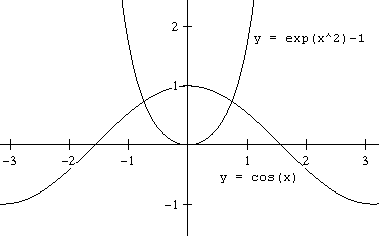
- Zaletą narzędzia
Szukaj wynikujest to, że nie wymaga od nas znajomości wzoru na pierwiastki równania.
Nie wymaga nawet by wzór istniał – równanie jest rozwiązywane numerycznie. - Wadą jest to, że znajduje tylko jeden pierwiastek, niekoniecznie ten, który nas interesuje.
Rozwiązywanie
- Przekształcamy równanie tak, by po prawej równania było $0$: $e^{x^2}-1-\cos x = 0$.
- Wybieramy komórkę (np.
C3), do której program wpisze rozwiązanie. Wpisujemy do niej dowolną liczbę. W Excelu komórka może być pusta. - Do dowolnej komórki (np.
C4) wpisujemy formułę – lewą stronę równania. Niewiadomą $x$ zastępujemy adresem komórki z poprzedniego kroku, wyrażenie matematyczne zapisujemy w formacie właściwym dla arkusza:=exp(potęga(C3; 2)) - cos(C3) - 1
- Uruchamiamy narzędzie
Szukaj wyniku:
Calc:Narzędzia ⇒ Szukaj wyniku
Excel:Dane ⇒ Analiza warunkowa ⇒ Szukaj wyniku - W formularzu wypełniamy wszystkie pola:
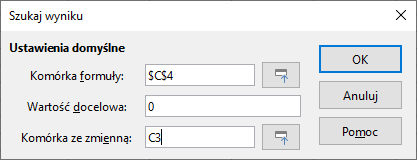
- Po zatwierdzeniu, w komórce
C3pojawi się wynik – liczba $0,74288771114532$.
Inne pierwiastki
Równanie $e^{x^2}-1-\cos(x)=0$ ma dwa – różniące się znakiem – pierwiastki. Narzędzie Szukaj wyniku znajduje jeden z nich, ten dodatni. W przypadku tego równania
możemy łatwo ustalić wartość drugiego pierwiastka. Taka sytuacja nie jest typowa, jesteśmy zazwyczaj „skazani” na jeden pierwiastek, niekoniecznie ten, który nas interesuje.
Rozważmy równanie $\sin(x) = \frac{1}{2}x$
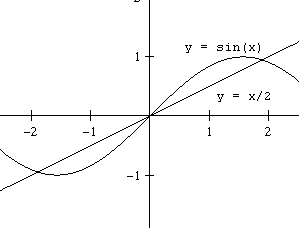
Szukaj wyniku znajdzie oczywiste rozwiązanie $x=0$. Co zrobić jeżeli interesuje nas najmniejszy pierwiastek dodatni? Rozpatrzmy nową funkcję,
nazwijmy ją sinus, której wykres częściowo (dla $x\ge 0,5$) pokrywa się z wykresem funkcji $\sin$.
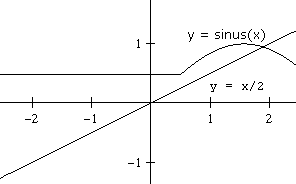
Pierwiatek równania $sinus(x)-\frac{1}{2}x=0$ jest szukanym najmniejszym pierwiastkiem równania $\sin(x) = \frac{1}{2}x$
Nadal zakładamy, że program ma wpisać rozwiązanie do komórki C3.
Do komórki z formułą (np. C4) wpisujemy:
=JEŻELI(C3 <= 0,5 ; 0,5 ; sin(C3)) - C3/2
Szukaj wyniku, program znajduje rozwiązanie, liczbę $1,89549313523737$.
Inny sposób zdefiniowania funkcji sinus, to napisanie makra. Oznacza to „nauczenie” arkusza nowej funkcji.
Aby napisać makro, musimy otworzyć okno edytora makr:
- Calc:
Narzędzia ⇒ Makra ⇒ Zarządzaj makrami ⇒ Basic ⇒ Edycja - Excel:
Deweloper ⇒ Makra
Standardowo kartyDewelopernie ma na wstążce. Trzeba ją dodać:Plik ⇒ Opcje ⇒ Dostosowywanie wstążki
W oknie edytora wpisujemy kod funkcji:
Function sinus(x As Double) As Double If x <= 0.5 Then sinus = 0.5 Else sinus = sin(x) End If End Function
Nadal zakładamy, że program ma wpisać rozwiązanie do komórki C3.
Do komórki z formułą (np. C4) wpisujemy
=sinus(C3) - C3/2
Uruchamiamy narzędzie Szukaj wyniku, program znajduje rozwiązanie, liczbę $1,89549413529882$.
Filtrowanie
Filtr to zestaw warunków, które musi spełniać zawartość komórek by wiersz został wyświetlony.
Do testowania filtrów można wykorzystać plik Panstwa.xlsx.
Przykładowy zestaw warunków: państwa leżące w Afryce lub w Europie, których powierzchnia przekracza 1000 km2.
Oba programy (Excel i Calc) mają trzy narzędzia filtrujące różniące się dopuszczalną budową warunków:
- autofiltr
- filtr standardowy
- filtr zaawansowany
Autofiltr
Warunek dotyczący kolumny ma postać:
(zawartość komórki = wartość)$\vee\dots\vee$(zawartość komórki = wartość).
Warunek końcowy jest koniunkcją warunków dotyczących kolumn.
Np. państwa leżące w Afryce, w których językiem urzędowym jest angielski, arabski lub francuski.
(w Afryce)$\wedge$((język=angielski)$\vee$(język=arabski)$\vee$(język=francuski))
Filtr standardowy
Filtr standardowy – warunek dotyczący kolumny ma postać:
- zawartość komórki = «wartość»
- zawartość komórki ≤ «wartość»
- zawartość komórki zawiera «wartość»
- …
Warunek końcowy jest koniunkcją, alternatywą lub jednym i drugim warunków dotyczących kolumn.
Np. państwa leżące w Europie, w których jednym z języków urzędowych jest angielski lub liczba ludności ≥ 10 mln.
(w Europie)$\wedge$((język zawiera angielski)$\vee$(ludność ≥ 10 mln.))
Tworząc filtr standardowy nie mamy niestety możliwości wpisania nawiasów. Powstanie zatem taki (beznawiasowy) warunek:
(w Europie)$\wedge$(język zawiera angielski)$\vee$(ludność ≥ 10 mln.)
Zgodnie z priorytetami operatorów logicznych (wpierw koniunkcja, potem alternatywa) będzie on interpretowany (niezgodnie z intencją) tak:
((w Europie)$\wedge$(język zawiera angielski))$\vee$(ludność ≥ 10 mln.)
Filtr zaawansowany
Filtr zaawansowany opisujemy gdzieś w dokumencie (skoroszycie), który chcemy filtrować. Można wykorzystać fragment filtrowanego arkusza, można wykorzystać inny arkusz.

- Puste komórki w obszarze filtru oznaczaja brak warunku.
- Wypełnione komórki w jednym wierszu są łączone operatorem koniunkcji:
- (w Europie)$\wedge$(język = angielski),
- (w Europie)$\wedge$(ludność ≥ 10).
- Wiersze są łączone operatorem alternatywy.
Równoważnie i trochę krócej:
(w Europie)$\wedge$((język = angielski)$\vee$(ludność ≥ 10))
Kłopoty sprawia zapisanie innego niż równość, warunku dotyczącego komórek z tekstem. Jak zapisać np. warunki, że język zawiera angielski lub, że angielski jest ostatnim wymienionym językiem? Rozwiązaniem są tzw. wyrażenia regularne. Są one potężnym narzędziem do składniowej analizy tekstu. Ważny przykład wyrażenia regularnego: .*, oznacza ono dowolny (również pusty!) ciąg znaków. W konsekwencji:
- .*angielski.* oznacza ciąg znaków zawierający słowo angielski,
- .*angielski oznacza ciąg znaków kończący się słowem angielski.
- ma.*ma oznacza ciąg znaków zaczynający się i kończący sylabą ma.
Pytania sprawdzające
Pytania dotyczą pliku Panstwa.xlsx.
Narzędzie Solver
Narzędzie Solver ma kilka zastosowań:
- Wyznaczanie największej wartości funkcji wielu zmiennych $y=f(x_1,\dots,x_n)$. Dziedzina funkcji jest opisana układem równań i nierówności.
- Wyznaczanie najmniejszej wartości najmniejszej dla funkcji wielu zmiennych $y=f(x_1,\dots,x_n)$. Również teraz dziedzina funkcji jest opisana układem równań i nierówności.
- Rozwiązywanie układu równań i nierówności.
W programie Calc narzędzie Solver jest zawsze dostępne (Narzędzia ⇒ Solver).
W programie Excel może być konieczne zainstalowanie dodatku Solver oraz dołączenie go do Excela: Plik ⇒ Opcje.
Po dołączeniu, narzędzie Solver jest dostępne na karcie Dane.
Funkcje jednej zmiennej
Wyznaczymy największą wartość funkcji $y=sin(\frac{1}{3}x)$ dla $30^\circ\le x \le 300^\circ$.
Do dowolnej komórki arkusza (np. B14) wpisujemy formułę z powyższego wzoru.
W programach Excel i Calc funkcje trygonometryczne oczekują argumentów w radianach. Jeżeli chcemy posługiwać się stopniami, to musimy skorzystać z funkcji
radiany() przeliczającej stopnie na radiany.

Uruchamiamy narzędzie Solver:
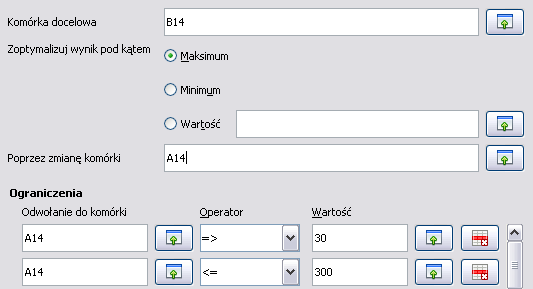
Informujemy program, w której komórce jest formuła (B14), w której jest zmienna (A14), jakie są ograniczenia na zmienną i czym jesteśmy zainteresowani (maksimum).
Zatwierdzamy i w komórkach A14 oraz B14 pojawia się rozwiązanie.

Funkcje wielu zmiennych
Na odcinku $\overline{AB},\, A = (-1;\,1),\, B = (3;\,2)$ wyznaczymy punkty leżące najdalej i najbliżej od początku układu. Najpierw, korzystając z kartki, napiszemy równanie
prostej przechodzącej przez punkty $A,\,B$, ma ono postać $4y-x-5=0$. By znaleźć punkt najbliższy i najdalszy, znajdziemy punkty, w których funkcja
$f(x,\,y)=x^2+y^2$ osiąga wartość największą i najmniejszą. Zmiennym $x,\,y$ przydzielimy komórki A9 i B9. Do komórki C9 wpiszemy formułę
opisującą badaną funkcję, a do komórki D9 formułę opisującą równanie prostej.

Uruchamiamy narzędzie Solver:
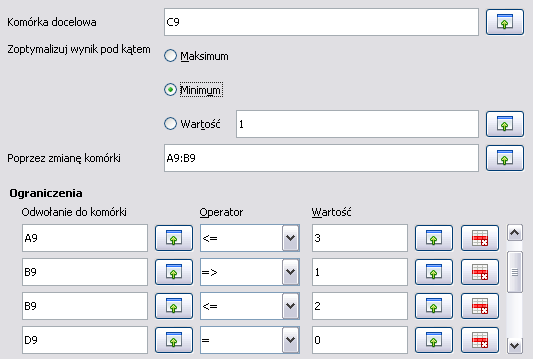
Zatwierdzamy i w komórkach A9:B9 pojawia się rozwiązanie.

Analogicznie możemy wyznaczyć punkt najdalszy.

Znalezione rozwiązanie pokazuje, że Solver korzysta z algorytmów przybliżonych. Pozwala to rozwiązać znacznie więcej zagadnień, ale w prostych przypadkach
może dawać gorsze rozwiązania. W opisywanym zagadnieniu wystarczy naszkicować rysunek, by zobaczyć, że punktem najdalszym jest punkt $(3;\,2)$.
Układy równań
Rozwiążemy układ równań$\begin{cases} x\cdot y\cdot z=1 \\x+y+z=0 \\x+2\cdot y+3\cdot z=0\end{cases}$
Każde równanie w układzie musi być postaci $f(x_1,\,\dots,\,x_n)=c$.
Niewiadomym z równania ($x,y,z$) przydzielamy komórki w arkuszu (np. A18, B18, C18). Formuły opisujące lewe strony równań wpisujemy do
dowolnych komórek arkusza (np. D18, E18, F18).

Uruchamiamy narzędzie Solver:
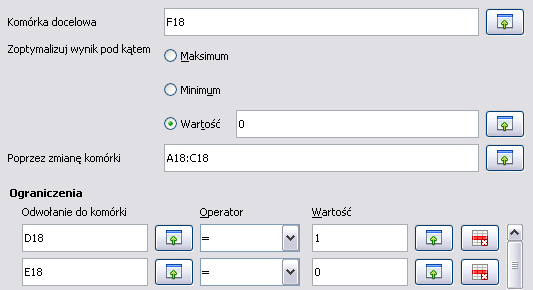
W polu Komórka docelowa wpisujemy adres jednej z komórek z formułą – nie ma znaczenia której. Zatwierdzamy i w komórkach A18:C18 pojawia się
rozwiązanie.
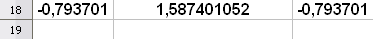
Pytania
- Na krzywej o równaniu $\frac{(x-2)^2}{4}+y^2=1\,\,\,\,(1)$
chcemy, korzystając z narzędzia
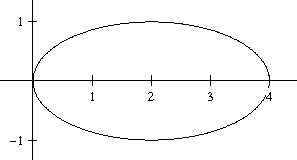
Solver, znaleźć jeden z punktów leżących najdalej od początku układu.Dlaczego wyznaczenie maksimum funkcji $f(x,\,y)=x^2+y^2$ przy ograniczeniach $\begin{cases}0\le x\le 4\\0\le y\le 1\\x^2-4x+4y^2=0\,\,\,\,(2)\end{cases}$ da nam rozwiązanie?
Wyjaśnienie - Korzystając z narzędzia
Solver, chcemy wyznaczyć współrzędne zaznaczonego punktu przecięciakrzywych $y=\frac{x}{2}+1\,\,\,\,y=2\cos(x)$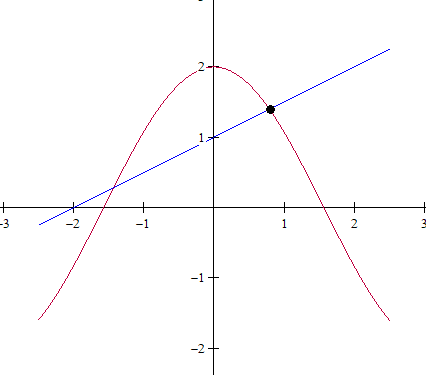
Do arkusza wpisaliśmy:Uruchamiamy narzędzie
Solver.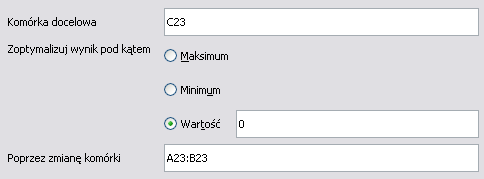 Wyjaśnienie
Wyjaśnienie - Producent dostał zamówienie na 1000 sztuk pewnego produktu. Produkt występuje w dwóch odmianach:
- odmiana
p1, koszt produkcji 10 zł., czas produkcji 5 minut - odmiana
p2, koszt produkcji 5 zł., czas produkcji 8 minut
Zawartość arkusza:
Uruchamiamy narzędzie
Solver.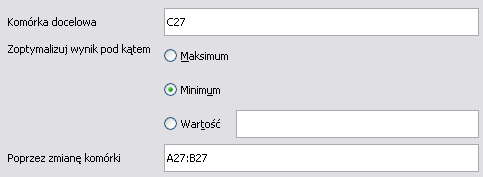 Wyjaśnienie
Wyjaśnienie - odmiana