Program Scilab

Program Scilab jest darmowy. Można go pobrać ze strony https://www.scilab.org/download/scilab-6.1.1.

Uruchamianie

Aby uruchomić program wyszukujemy ikonę na pulpicie lub odpowiednią pozycję w menu programów. Pojawi się okno interfejsu graficznego:

W tym oknie możemy, za znakiem zachęty

wpisywać polecenia.
Poprzez menu mamy dostęp do pomocy (po angielsku), przykładów i edytora SciNotes.

Polecenia można wpisywać na dwa sposoby:

zm = polecenie, np. $x=34/55$
polecenie, np $34/55$

W obu przypadkach polecenie zostanie wykonane, wynik polecenia zostanie wypisany na ekran (jeżeli nie zakończymy polecenia średnikiem) i zapamiętany: w pierwszym przypadku zostanie zapamiętany w zmiennej o nazwie zm, w drugim w zawsze istniejącej zmiennej o nazwie ans.
Przykład:

x = 12/13 ⇒ 0.9230769
y = 13/14; ⇒ nic się nie pojawi z powodu średnika na końcu
14/15 ⇒ 0.9333333
x + y + ans ⇒ 2.7849817

Nie każde polecenie ma jakiś wynik – zwraca jakąś wartość. Na przykład polecenie wyświetlające disp niczego nie zwraca:

s = disp("Witaj świecie!") ⇒ Witaj świecie!
s ⇒   !--error 4 Niezdefiniowana zmienna: s

Tablice

W programie Scilab działa się właściwie na tablicach liczb o rozmiarze $w\times k$, $w$ jest ilością wierszy, $k$ ilością kolumn. Ważny przypadek szczególny, to tablica o rozmiarze $1\times 1$, utożsamiana z jedyną znajdującą się w niej liczbą.

Konsekwencją takiego podejścia jest ogromna ilość poleceń tworzących tablice.

Tworzenie tablic

```
A = [1 2 3;4 5 6] ⇒
1 2 3
4 5 6
```
Sposób bardzo niewygodny przy tworzeniu dużych tablic – wszystkie elementy musimy wpisać. Średnik jest separatorem wierszy.
```
A = a:b      
A = 5.2:9.5 ⇒ 5.2  6.2  7.2  8.2  9.2
```
Powstaje tablica jednowierszowa (wektor), wyrazy tworzą ciąg arytmetyczny o różnicy $1$, pierwszy wyraz jest równy $a$, ostatni ≤ $b$.
```
A = a:r:b      
A = 5.2:0.7:9.5 ⇒ 5.2  5.9  6.6  7.3  8.  8.7
```
Powstaje tablica jednowierszowa (wektor), wyrazy tworzą ciąg arytmetyczny o różnicy $r$, pierwszy wyraz jest równy $a$, ostatni ≤ $b$.
```
A = linspace(a,b,n)      
A = linspace(0,%pi,5) ⇒ 0.  0.7853982  1.5707963  2.3561945  3.1415927
```
Powstaje tablica jednowierszowa (wektor), wyrazy tworzą $n$-elementowy ciąg arytmetyczny, pierwszy wyraz jest równy $a$, ostatni $b$.
```
A = zeros(w,k)
B = ones(w,k)
C = rand(w,k)
```
Powstaną trzy tablice o rozmiarze $w\times k$, tablica $A$ zawiera same zera, tablica $B$ same jedynki, a tablica $C$ zawiera liczby losowe z przedziału $[0;\,1)$.

Opisane wyżej sposoby można łączyć:

E = 1:100 ⇒ 1 2 3 ... 100
F = 101:200 ⇒ 101 102 103 ... 200
A = [E;F] ⇒
1   2   3 ... 100
101 102 103 ... 200

Często potrzebne są tablice jednokolumnowe, wygodnym narzędziem do ich tworzenia jest operator transpozycji $'$ (apostrof), który zamienia wiersze na kolumny, a kolumny na wiersze.

w = linspace(0,1,101) ⇒  0. 0.01  0.02  0.03 ... 0.98  0.99  1.
v = w' ⇒
0.    
0.01  
0.02  
0.03
...

Utwórz tablicę dwuwymiarową o rozmiarze $100\times 2$, która w pierwszej kolumnie zawiera same zera, a w drugiej same jedynki.

Rozwiązanie

A = [zeros(1,100);ones(1,100)]'

Ukryj

Funkcje na tablicach

Jeżeli $f$ jest funkcją jednej zmiennej liczbowej (np. $f(x)=\sin(x)$), a $A$ jest tablicą liczb rozmiaru $w\times k$, to polecenie

B = f(x)

utworzy nową tablicę – również rozmiaru $w\times k$. Liczby w tej tablicy, to wartości funkcji $f$ na liczbach z tablicy $A$.

A = 0:30:90 ⇒ 0.  30.  60.  90.
C = [A;sind(A);sin(A)] ⇒
0.    30.          60.          90.        
0.    0.5          0.8660254    1.         
0.  - 0.9880316  - 0.3048106    0.8939967

W Scilabie są dwie funkcje sinus, funkcja $\sin$ oczekująca argumentu w radianach i funkcja $\text{sind}$ oczekująca argumentu w stopniach (degree). Analogicznie, istnieją dwie funkcje cosinus $\cos$ i $\text{cosd}$, dwie funkcje tangens $\tan$ i $\text{tand}$ oraz dwie funkcje cotangens $\cot$ i $\text{cotd}$.

Analogicznie zachowują się operatory arymetyczne i operator potęgowania.

A = linspace(0,10,6) ⇒ 0.  2.  4.  6.  8.  10.
A + 5 ⇒ 5.  7.  9.  11.  13.  15.
A.^0.5 ⇒ 0.  1.4142136  2.  2.4494897  2.8284271  3.1622777

W wersji 5.5 Scilaba można było operator potęgowania tablicy zapisać odrobinę krócej A^0.5 (bez kropki za symbolem tablicy).

Operatory arytmetyczne i operator potęgowania można zastosować również do dwóch tablic. Obie tablicy muszą mieć taki sam rozmiar, działania wykonywane są wyraz po wyrazie.

A = 1:4 ⇒ 1.  2.  3.  4.
B = 2:5 ⇒ 2.  3.  4.  5.
A+B     ⇒ 3.  5.  7.  9.
A.^B    ⇒ 1.  8.  81.  1024.
A.*B    ⇒ 2.  6.  12.  20.

Operatory potęgowania, mnożenia i dzielenia trzeba pisać z kropką (A.*B) – istnieją – ważne w algebrze liniowej – operatory mnożenia i dzielenia bez kropki. Działaja zupełnie inaczej i wymagają innych zależności między rozmiarami tablic.

A*B ⇒ !--error 10 Niezgodne mnożenie.

Istnieją też funkcje, które działają na całej tablicy, a nie na poszczególnych jej wyrazach.

max(A) zwraca największą liczbę w tablicy
min(A) zwraca najmniejszą liczbę w tablicy
sum(A) zwraca sumę liczb w tablicy
prod(A) zwraca iloczyn liczb w tablicy
length(A) zwraca ilość liczb w tablicy

Utwórz tablicę rozmiaru $5\times 4$ zawierajacą losowe liczby całkowite z przedziału $[0;\,9]$. Oblicz wartość średnią liczb w tablicy.
Wskazówka, przydatna będzie funkcja $\text{floor}(x)$ zaokrąglająca w dół.

Rozwiązanie

A = floor(9*rand(5,4))
avg = sum(A)/length(A)

Ukryj

Proste zastosowania

Rozwiązywanie układów równań liniowych. Układ równań

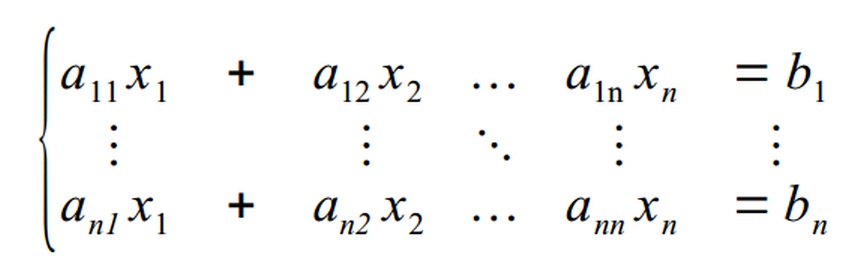
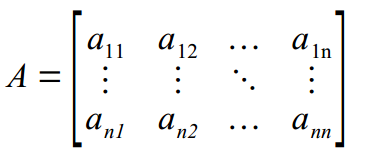
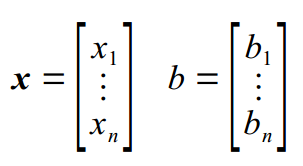
możemy za pomocą macierzy (tablicy) $A$ rozmiaru $n\times n$ oraz wektorów jednokolumnowych $x$ i $b$

zapisać w postaci $A\cdot x=b$. Zapis ten sugeruje, że aby otrzymać $x$ trzeba $b$ podzielić przez $A$. Rzeczywiście, rozwiążemy układ: $\begin{cases}x+y+z=6\\x+y-z=0\\x-y-z=-4\end{cases}$

A = [1 1 1;1 1 -1;1 -1 -1]
b = [6 0 -4]' 
x = (A\b)' ⇒ 1.  2.  3.

Dwukrotnie odbyła się transpozycja: wektor $b$ musi być kolumnowy, rozwiązanie chciałem wyświetlić w jednym wierszu.

Obliczanie pierwiastków wielomianu. W programie Scilab wielomiany tworzymy poleceniem poly(A,zm,[flaga]), gdzie $A$ jest jednowierszową tablicą liczb, $zm$ jest symbolem zmiennej, nieobowiązkowy parametr $flaga$ decyduje czy liczby z wektora $A$ są współczynnikami wielomianu (flaga='c'), czy pierwiastkami (flaga='r'). Domyślnie są pierwiastkami. Do obliczenia pierwiastków wielomianu $w$ służy polecenie roots(w).

A = 1:5 ⇒ 1.  2.  3.  4.  5.
w = 0.5*poly(A,'y','c') ⇒ 0.5 + y + 1.5y² + 2y³ + 2.5y⁴   
roots(w) ⇒
0.1378323 + 0.6781544i  
0.1378323 - 0.6781544i  
- 0.5378323 + 0.3582847i  
- 0.5378323 - 0.3582847i

Wszystkie pierwiastki są zespolone.

Sporządzanie wykresów funkcji jednej zmiennej. Wykres rysujemy poleceniem plot2d(wektor_x,wektor_y), wektor_x i wektor_y muszą być wektorami tej samej długości. Wykres funkcji $y=\sin(x^2)$ na przedziale $[0;\,2\cdot\pi]$ uzyskujemy tak:

x = linspace(0,2*%pi,201);
y = sin(x.*x);
plot2d(x,y)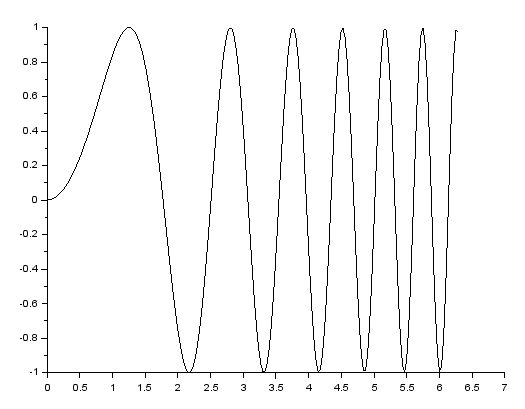

Polecenie rysujące plot2d dostaje tylko ciąg punktów, nie dostaje informacji jak ten ten ciąg powstał, nie może zatem opisać wykresu. O opisanie wykresu musi zadbać użytkownik programu.

Krzywe płaskie

Wykresy funkcji

Do umieszczania napisów w oknach graficznych (do opisywania rysunków) służy polecenie xstring(x,y,tekst). Liczby $x$ i $y$, to współrzędne lewego dolnego rogu napisu, tekst może zawierać wzory matematyczne w formacie LaTeXa. Podczas wpisywania wzoru, w konsoli Scilaba pojawia się podgląd przetworzonego wzoru: .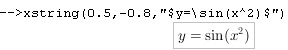
Wykres funkcji $y=\sin(x^2)$ uzupełniony o powyższy napis wygląda tak:

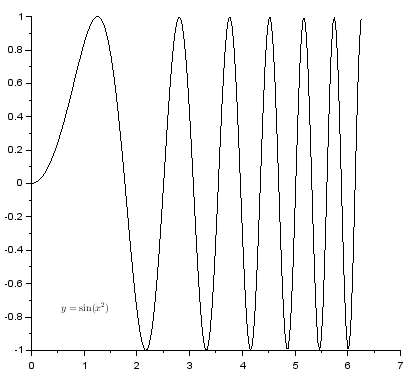
Kolejne polecenia plot2d rysują w tym samym oknie. Dopasowują jednocześnie skalowanie osi do wszystkich krzywych. Wykres funkcji $y=\sin(x^2)$ uzupełniony poleceniami

y2 = exp(x);
plot2d(x,y2)

o wykres funkcji $y=e^x$ wygląda tak:

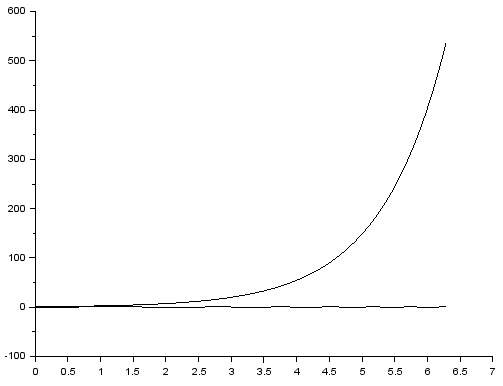
Domyślne zachowanie programu możemy zmienić poleceniem set("własność",nowa_wartość).
Kilka przydatnych wersji polecenia set:

set("auto clear","on") – kolejne polecenie rysowania usuwa dotychczasowe krzywe
set("window",nr) – kolejne polecenie rysowania rysuje w oknie o podanym numerze $nr$, domyślnie rysowanie odbywa się w oknie o numerze $0$
set("thickness",nr) – zmienia grubość linii
set("default") – przywraca ustawienia domyślne

Polecenie subplot(w,k,which) dzieli (wirtualnie) okno graficzne na $w\cdot k$ równych części, $w$ to ilość wierszy, $k$ ilość kolumn.
Parametr $1\le which\le w\cdot k$ wskazuje, w której części chcemy rysować.

x = linspace(0,2*%pi,301);
y = sin(x.*x);    
subplot(2,2,1)
plot2d(x,y)
subplot(2,2,2)
plot2d(x,y)
subplot(2,1,2)
plot2d(x,y) ⇒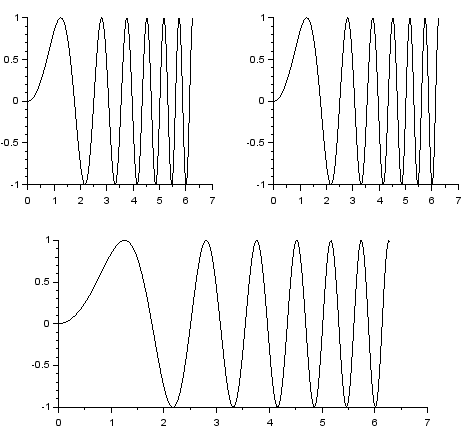

Krzywe parametryczne i łamane

Wszystkie dotychczasowe rysunki były wykresami funkcji $y=f(x)$. Wynikało to ze sposobu przygotowania danych dla polecenia plot2d(x,y) – wektor $x$ tworzony poleceniem linspace(...) jest rosnący. Możliwe są też inne rysunki.

Krzywa parametryczna, tzn. krzywa opisana równaniami $\begin{cases}x=f(t)\\y=g(t)\end{cases}$.
Przykład krzywej parametrycznej (kardioida):

t = linspace(0,2*%pi,301);
x = sin(t).*(1+cos(t));
y = 2-cos(t).*(1+cos(t));
plot2d(x,y)
xtitle("$Kardioida \begin{cases}x=\sin(t)\cdot (1+\cos(t))\\y=2-\cos(t)\cdot(1+\cos(t))\end{cases}$") ⇒

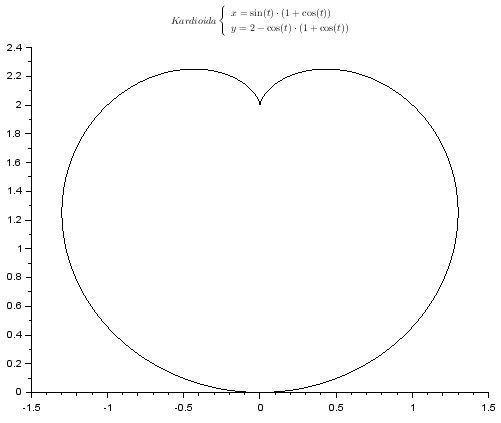
Geometryczna definicja kardioidy – krzywa zakreślana przez ustalony punkt okręgu toczącego się po zewnętrzu innego okręgu.
Polecenie xtitle("tytuł") wyświetla tytuł nad rysunkiem i jak widać, akceptuje składnię LaTeXa.

W rzeczywistości, polecenie plot2d(x,y) rysuje łamaną: zaznacza opisane w wektorach $x$ i $y$ punkty i łączy je odcinkami. Jeśli punktów jest dużo, to segmenty łamanej są krótkie i widzimy ją w postaci krzywej.
Narysujemy teraz łamaną, która ma tylko sześć punktów, szósty punkt jest identyczny z pierwszym.

t = linspace(0,2*%pi,6);
y = cos(t);
x = sin(t);
plot2d(x,y)
xtitle("Pięciokąt foremny") ⇒

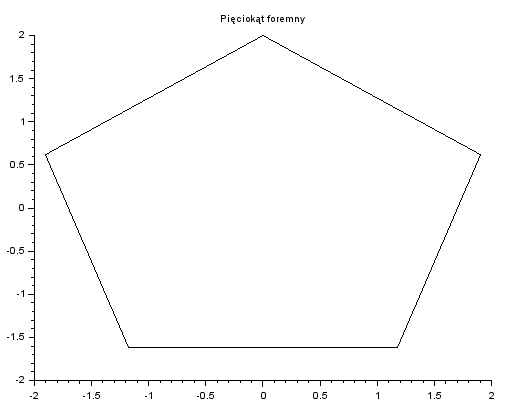
Do rysowania łamanych często wykorzystywane jest polecenie plot2d4(x,y), polecenie to, opisane wektorami $x$ i $y$ punkty łączy strzałkami. Wykorzystam wektory $t$, $x$ i $y$ z poprzedniego przykładu do narysowania grafu skierowanego.

plot2d4(x,y)
plot2d4([0 x(1)],[0 y(1)])
plot2d4([x(3) 0],[y(3) 0])
plot2d4([x(4) 0],[y(4) 0])
xtitle("Graf skierowany") ⇒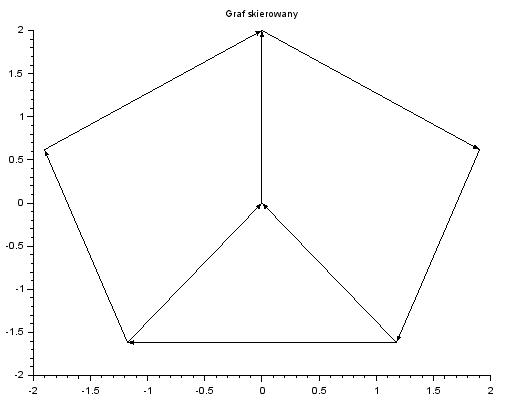

Wyrażenie $x(n)$ oznacza $n$-tą współrzędną wektora $x$ – numeracja zaczyna się od $1$. Wyrażenie x(p:k) oznacza podciąg wektora $x$ zaczynający się na miejscu $p$, a kończący na miejscu $k$.

a = 1:6 ⇒ 1.  2.  3.  4.  5.  6.
a(3)    ⇒ 3.
a(2:4)  ⇒ 2.  3.  4.

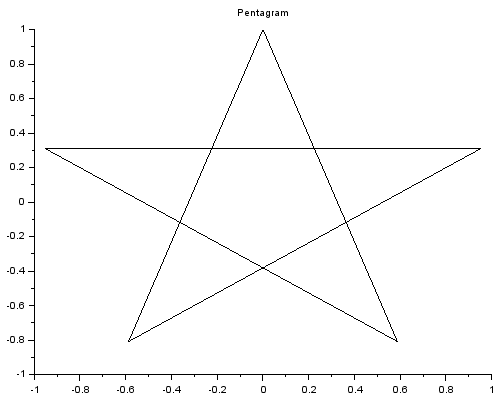
Narysuj pentagram. Pentagram można otrzymać z wierzchołków pięciokąta foremnego, łącząc co drugi wierzchołek.

Rozwiązanie

t = linspace(0,2*%pi,6);
y = cos(t);
x = sin(t);
plot2d([x(1) x(3)],[y(1) y(3)])
plot2d([x(3) x(5)],[y(3) y(5)])
plot2d([x(5) x(2)],[y(5) y(2)])
plot2d([x(2) x(4)],[y(2) y(4)])
plot2d([x(4) x(1)],[y(4) y(1)])
xtitle("Pentagram") ⇒

Ukryj

Podobieństwo pięciu instrukcji rysujących z powyższego zadania sugeruje, że życie byłoby prostsze gdybyśmy mieli do dyspozycji pętle.

Programowanie

Skrypty (programy) najwygodniej jest pisać w edytorze SciNotes, jest on dostępny z głównego menu Narzędzia ⇒ SciNotes. Wpisanego skryptu nie można uruchomić przed zapisaniem na dysk.

Po zapisaniu, można skrypt uruchomić np. klikając w przycisk Wykonaj

lub (bez pośrednictwa edytora SciNotes) wybierając w menu Plik ⇒ Otwórz plik.

Wszystkie polecenia, których możemy użyć w skrypcie, możemy też wpisać na konsoli. Podstawowe zalety skryptów:

przy działaniach wykonywanych wielokrotnie wpisujemy polecenia tylko raz
łatwość poprawiania, jeśli wykonywane zadanie wymaga $13$ poleceń, a niepoprawnie wpisaliśmy na konsoli drugie polecenie, to musimy wpisać poprawną wersję drugiego i wszystkie polecenia od trzeciego do trzynastego

Pętle

Pętla for, podstawowa forma wygląda tak ($i$ jest zmienną sterującą pętli, $w$ wektorem):

for i = w
instrukcja 1;
...
end

Dwa przykłady.

zsumowanie wszystkich liczb nieparzystych z przedziału $[1;\,100]$ oraz ich odwrotności
```
suma = 0
odw = 0
for i = 1:2:100
  suma = suma + i;
  odw = odw + 1/i;
end
```

narysowanie poniższej figury

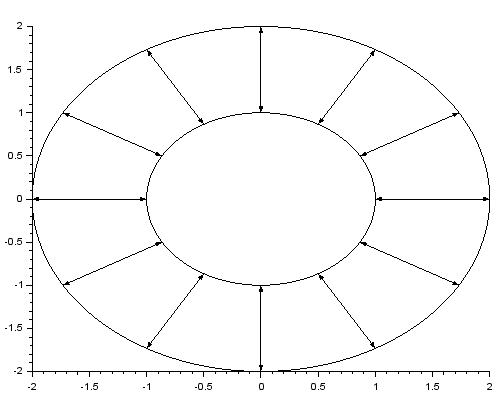
t = linspace(0,2*%pi,201);
x = cos(t);
y = sin(t);
plot2d(x,y) ⇒ mniejszy okrąg
plot2d(2*x,2*y) ⇒ mniejszy okrąg
t = linspace(0,2*%pi,13);
x = cos(t);
y = sin(t);
for i = 1:12
  plot2d4([x(i) 2*x(i)],[y(i) 2*y(i)]) ⇒ strzałki "odśrodkowe"
  plot2d4([2*x(i) x(i)],[2*y(i) y(i)]) ⇒ strzałki "dośrodkowe"
end

Pętla while, podstawowa forma wygląda tak:

while(warunek)
  instrukcja 1;
  ...
end

Dla danej liczby dodatniej $a$ szukamy najmniejszej liczby postaci $2^n$ takiej, że $a<2^n$

x = 1
while(x <= a)
  x = 2*x;
end

Instrukcje sterujące

Instrukcje sterujące umożliwiają „rozwidlenie” skryptu (programu), jeśli spełnione są pewne warunki, to skrypt wykonuje pewien zestaw instrukcji, jeśli nie są spełnione, to wykonuje inny zestaw. Wybór drogi, którą podąży skrypt zależy często od decyzji użytkownika.

Instrukcje umożliwiające interakcję skryptu z użytkownikiem, to:

disp(message) – wyświetla message
```
disp("Program robiący to i owo")
```
zm = input(prompt) – wyświetla prompt, czeka na wpisanie czegoś (i naciśnięcie Enter), zapamiętuje w zmiennej zm co wpisał użytkownik
```
l = input("wpisz coś "); ⇐ 99
disp(l) ⇒ 99.
```

Instrukcja if-elseif-else. Ma ona trzy odmiany:

jest tylko jedna droga

x = input("wpisz liczbę ");
if (x>5)
  disp("wpisałeś liczbę większą niż 5")
end

są dwie drogi

x = input("wpisz liczbę ");
if (x>5)
  disp("wpisałaś liczbę większą niż 5")
else
  disp("nie wpisałaś liczby większej niż 5")
end

są co najmniej trzy drogi

x = input("wpisz liczbę ");
if (x>5)
  disp("wpisałeś liczbę większą niż 5")
elseif(x>3)
  disp("wpisałeś liczbę z przedziału (3;5]")
elseif(x>1)
  disp("wpisałeś liczbę z przedziału (1;3]")
...  
end

kaskada elseif może się kończyć klauzulą else.

Instrukcja select-case, uzależnia wykonanie kodu od wartości pewnej zmiennej.

disp("Program rysujący n-kąty foremne")
n = input("n = ")
select n
  case 3 then msg = "wybrałaś trojkąt"
  case 4 then msg = "wybrałaś kwadrat"
  case 5 then msg = "wybrałaś pięciokąt"
  ...
  else msg = "za mało lub za dużo boków"
end
disp(msg)

Zadania

Utwórz tablicę $A$ o rozmiarze $10000\times 2$, o takiej zawartości:

1         0.2224478
1001      0.4957695
2001      0.4998512
3001      0.5056818
...
98001     0.5007329
99001     0.500273
10000     0.4991944

Jeżeli $n$ oznacza liczbę w pierwszej kolumnie, to liczba w drugiej kolumnie jest średnią arytmetyczną $n$ losowo wybranych liczb z przedziału $[0;\,1)$. Przydatna może być funkcja mean(A) wyliczająca średnią wartość liczb z tablicy $A$.

Rozwiązanie

A = []
for i = 1:10000
  A = [A [i;mean(rand(i,1))]]
end
A = A'

Zaczynamy od pustej tablicy ($A=[]$), potem w pętli dopisujemy z prawej strony tablicę o rozmiarze $2\times 1$.

Ukryj

Utwórz tablicę $B$ o rozmiarze $3\times 101$.

Pierwszy wiersz ma zawierać $101$ wylosowanych liczb całkowitych z przedziału $[0;\,1000]$.
Drugi wiersz ma zawierać liczby z pierwszego wiersza uporządkowane malejąco.
Trzeci wiersz ma zawierać liczby z pierwszego wiersza uporządkowane rosnąco.

Wypisz medianę liczb z pierwszego wiersza.

Rozwiązanie

B = floor(1001*rand(1,101))
A = [B;gsort(B);gsort(B,'g','i')]
disp(A(2,51))

Funkcja rand(1,101) utworzy tablicę o rozmiarze $1\times 101$ zawierającą liczby losowe z przedziału $[0;\,1)$. Po pomnożeniu przez $1001$ i zaokrągleniu w dół dostaniemy liczby całkowite z przedziału $[0,1000]$. Funkcja gsort bez parametrów sortuje malejąco, a z parametrami rosnąco. Sortowanie nie ma wpływu na wartość mediany, a po sortowaniu mediana jest w środku wektora.

Ukryj

Utwórz tablicę $C$ o rozmiarze $100\times 100$, taką, że liczba w wierszu $w$ i kolumnie $k$ ma wartość $w^2+k^2$.

Rozwiązanie

x = (1:100).*(1:100);
y = x;
x = x';
C = [];
for i = 1:length(y)
  C = [C y(i)+x];
end

Po utworzeniu, tablica $x$ jest jednowierszowa i zawiera kwadraty liczb całkowitych z przedziału $[1,100]$. Taką samą zawartość ma tablica $y$. W trzecim wierszu kodu, tablica $x$ staje sie (nie zmieniając zawartości) tablica jednokolumnową.

Ukryj

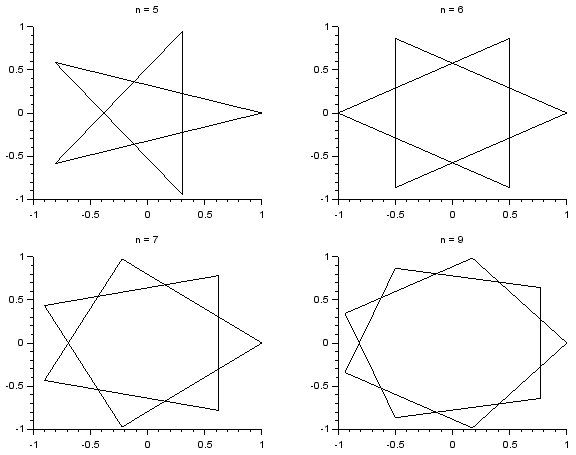
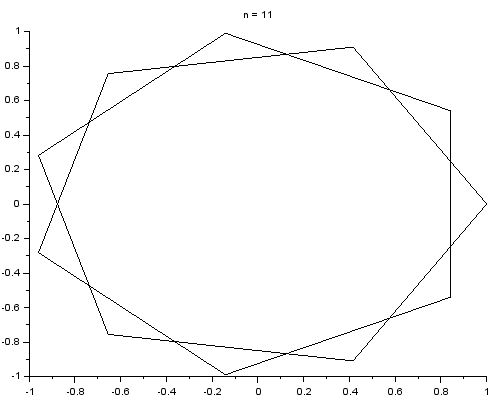
Napisz skrypt, który rysuje foremne wielokąty gwiaździste typu {n/2} (o wartość $n$ skrypt pyta użytkownika). Wielokąt foremny typu {n/2} powstaje przez połączenie co drugiego wierzchołka w zwykłym n-kącie foremnym.

Rozwiązanie

disp("Wielokąty gwiaździste (n,2)")
n = input("n = ")
t = linspace(0,2*%pi,n+1)
x = cos(t)
y = sin(t)
for i = 1:n
  next = i+2
  if (next > n+1) 
    next = 2
  end    
  plot2d([x(i) x(next)],[y(i) y(next)])
end
xtitle("n = "+string(n))

Zaczynamy od obliczenia współrzędnych wierzchołków (instrukcje t = ..., x = ..., y = ...). Następnie rysujemy odcinki łączące wierzchołki o numerach $i$ oraz $i+2$, kłopot pojawia się pod koniec – wektory mogą nie mieć współrzędnej o numerze $i+2$.

Po zapisaniu skryptu po nazwą polygons.sce w katalogu roboczym Scilaba, wpisaniu na konsoli kodu:

for k = 1:4
  subplot(2,2,k)
  exec('polygons.sce',-1)
end

i udzieleniu kolejno odpowiedzi $5,6,7,9$ otrzymamy taki rysunek:

Ukryj

Wykresy trójwymiarowe

Rysowanie krzywych

Krzywe rysujemy poleceniem param3d(wektor_x,wektor_y,wektor_z), wektory będące argumentami funkcji param3d muszą mieć taką samą długość. Takie podejście do rysowania wynika z tego, że krzywe w przestrzeni opisywane są zawyczaj parametrycznie

$\begin{cases}x=f_1(t)\\y=f_2(t)\\z=f_3(t)\end{cases}$

Wpierw przygotowujemy wektor parametrów $t$, następnie wyliczamy współrzędne wektorów $x$, $y$ i $z$.

t = linspace(0,8*%pi,601);
x = t.*cos(t);
y = t.*sin(t);
z = t;
param3d(x,y,z) ⇒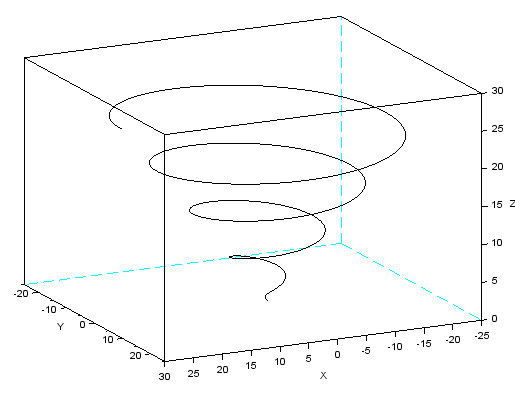

Rysunki trójwymiarowe w Scilabie można obracać (prawy przycisk myszy), powyższy wygląd narysowana krzywa uzyskała po wykonaniu obrotu.
Uzupełnimy rysunek o rzut krzywej na płaszczyznę $Oxy$. Funkcja zeros(tab) tworzy tablicę (wektor) o takim samym wymiarze jak tab, wypełnioną zerami.

param3d(x,y,zeros(z)) ⇒

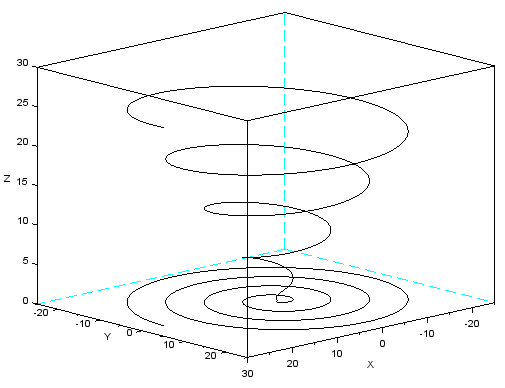
Polecenie param3d (analogicznie jak polecenie plot2d) rysuje łamaną.

x = [2 0 0 2]
y = [0 2 0 0]
z = [0 0 2 0]
set("thickness",3)
param3d(x,y,z) ⇒ osie i krzywa sa pogrubione
set("thickness",1) ⇒ przywraca cienkość osi

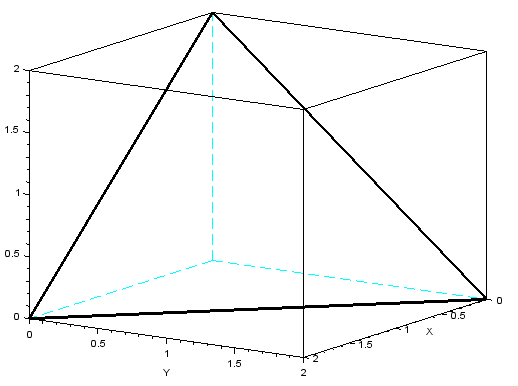
Rysowanie powierzchni

Powierzchnie rysujemy poleceniem plot3d(wektor_x,wektor_y,values_xy), długości wektorów wektor_x i wektor_y nie muszą byc równe, tablica values_xy musi mieć rozmiar $n_x\times n_y$, gdzie $n_x$ jest długością wektora wektor_x, a $n_y$ jest długością wektora wektor_y.

Sporządzenie wykresu funkcji $z=x^2+y^2,\,\,x,y\in [-2;\,2]$.

x = linspace(-2,2,201);
y = x;
z = zeros(201,201);
for w = 1:length(y)
  for k = 1:lenght(x)
    z(w,k) = y(w)^2 + x(k)^2;
  end
end
plot3d(x,y,z)

Jeżeli wzór na funkcję jest skomplikowany, to dla skrócenia zapisu warto zdefiniować własną funkcję.

Sporządzenie wykresu funkcji $z=\frac{\sin(x^2+y^2)}{x^2+y^2},\,\,x,y\in [-6;\,6]$.

function [w] = h(a,b)
  pom = a.*a + b.*b
  w = sin(pom)./pom
endfunction
x = linspace(-6,6,100);
y = linspace(-6,6,100);
z = zeros(100,100);
for w = 1:100
  for k = 1:100
    z(w,k) = h(x(w),y(k));
  end    
end
plot3d(x,y,z) ⇒

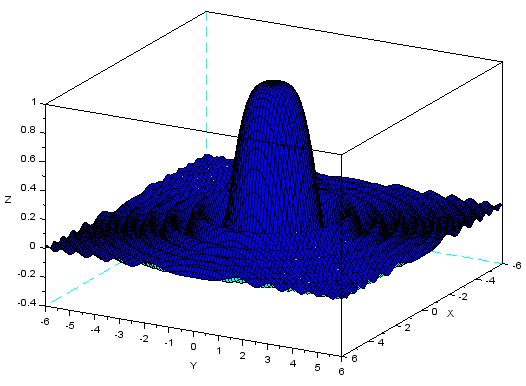
Zadania

Poniższy kod rysuje spiralę Archimedesa – krzywą o równaniu (we współrzędnych biegunowych) $r=\phi$.

t = linspace(0,8*%pi,401); 
x = t.*cos(t); 
y = t.*sin(t);
plot2d(x,y)
xtitle("Cztery zwoje spirali Archimedesa") ⇒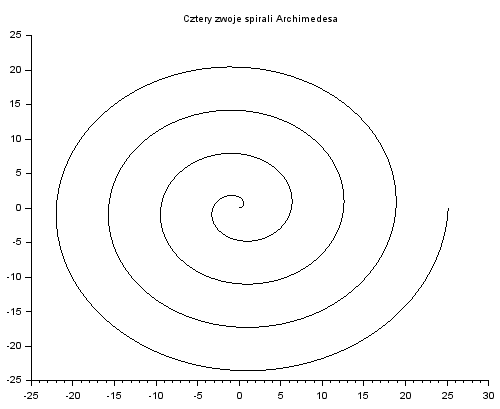

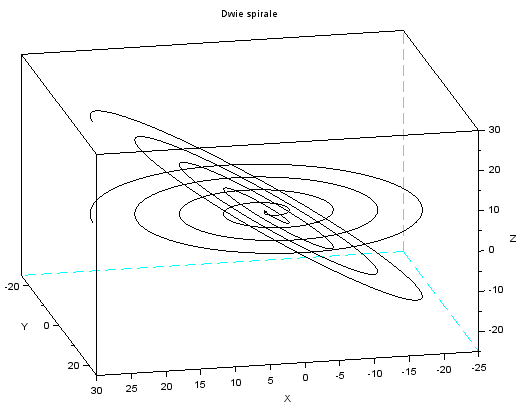
Narysuj w przestrzeni dwie spirale, jedna leży w płaszczyźnie $Oxy$ i jest krzywą z powyższego przykładu. Druga leży w płaszczyźnie o równaniu $z=x$, a jej rzutem na płaszczyznę $Oxy$ jest pierwsza krzywą.

Rozwiązanie

t = linspace(0,8*%pi,401); 
x = t.*cos(t); 
y = t.*sin(t);
param3d(x,y,zeros(x))
param3d(x,y,x)
xtitle("Dwie spirale") ⇒

Ukryj

Narysuj poniższą figurę – równoleżniki oddalone od siebie o 15° szerokości geograficznej.

Rozwiązanie

t = linspace(0,2*%pi,201);
x = cos(t);
y = sin(t);
for fi = linspace(-90,90,13)
  param3d(cosd(fi)*x,cosd(fi)*y,sind(fi)*ones(x))
end

Funkcje trygonometryczne $\text{cosd}$ i $\text{sind}$ oczekują argumentu w stopniach. Funkcja ones(tab) tworzy tablicę wypełnioną jedynkami o takim samym rozmiarze jak tab.

Ukryj

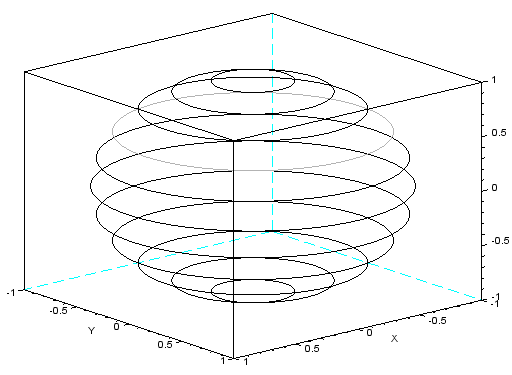
Narysuj odwócony stożek.

Rozwiązanie

Odwrócony stożek ma równanie $z=a\cdot\sqrt{x^2+y^2},\,\,a\gt 0$, wybierzmy $a=1$.

x = linspace(-4,4,201);
y = x;
z = zeros(201,201);
for w = 1:201
  for k = 1:201
    z(w,k) = sqrt(x(w)^2 + y(k)^2);
  end
end
plot3d(x,y,z)

Ukryj