Python jako kalkulator

Uruchamianie

Python jest potężnym językiem programowania i można pisać w nim programy o ogromnych możliwościach. Z Pythonem można również pracować interaktywnie, jest wówczas doskonałym narzędziem do wykonywania obliczeń matematycznych i sporządzania wykresów.

W Pythonie nie ma tzw. zgodności wstecz. W konsekwencji, niektóre polecenia mogą działać w nowej wersji Pythona inaczej niż działały w starej, a niektóre mogą w ogóle nie działać.
Najnowszą wersję Pythona z rodziny Python 3 można pobrać ze strony https://www.python.org/downloads/, a ostatnią wersję z rodziny Python 2 ze strony https://www.python.org/downloads/release/python-2717/.

Sposób uruchomiania zależy nieco od procesu instalacji.
Zazwyczaj są dwa sposoby uruchomienia:

„brzydsza” twarz Pythona, otwieramy konsolę i wpisujemy polecenie python
„ładniejsza” twarz Pythona, wyszukujemy ikonę na pulpicie lub odpowiednią pozycję w menu programów.

W trybie graficznym dostępny jest (po angielsku) bardzo przyjazny tutorial i bardzo rozbudowany help. W obu trybach Python czeka na wpisanie polecenia.

Uruchamianie programów

Listę poleceń (instrukcji) możemy zapisać do pliku. Powstanie wtedy program. W przyszłości – zamiast wpisywać listę poleceń – wystarczy wykonać program.
Do napisania programu możemy użyć dowolnego edytora (Notepad++, Emacs, Gedit, w ostateczności Notepad). Nazwa pliku z programem jest dowolna, natomiast rozszerzeniem winno być py. Sposoby uruchamiania programu:

podwójne kliknięcie w nazwę (ikonkę) pliku, wady: otwarte zostanie okno konsoli tekstowej, po wykonaniu programu okno to zostanie zamknięte uniemożliwiając odczytanie wyników, zamknięcie okna można wstrzymać kończąc program wierszem
```
raw_input("Press any key")
```
tekst w cudzysłowach może być inny,
otwarcie okna konsoli (w systemie Windows robimy to poleceniem cmd), wędrówka po folderach (polecenie cd ...) do folderu zawierającego program, wpisanie polecenia:
```
    python nazwa_programu
```
otwarcie okna graficznego i wybranie opcji: File ⇒ Open
po wybraniu pliku otwarte zostanie nowe okno
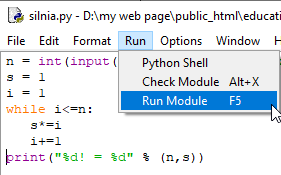
w którym wybieramy Run ⇒ Run Module.

Obliczenia

Operatory arytmetyczne

W liczbach separatorem dziesiętnym jest kropka.
Użycie przecinka między liczbami też jest dozwolone, ale przecinek nie jest wówczas separatorem – rozdziela kolejne wspólrzędne wektora.

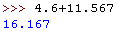
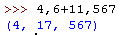
Po lewej stronie jest dodawanie liczb, po prawej jest wektor o trzech współrzędnych (druga z nich powstała przez dodawanie).

Operatory dodawania (+), odejmowania (-) i mnożenia (*) działają zgodnie z oczekiwaniami.

Działanie operatora dzielenia (/) jest trochę zaskakujące. Co więcej operator ten działa inaczej w Pythonie 2 a inaczej w Pythonie 3. Nieoczekiwane zachowanie dotyczy tylko dzielenia liczb całkowitych.

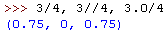Python 3:         Python 2: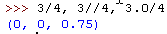 

Operator potęgowania ma nietypowy zapis (**) – by obliczyć $\sqrt 2$ wpisujemy 2**0.5.

Obliczenie $\sqrt[3]{-1}$

Szukamy liczb zespolonych (punktów) $z_1, z_2, z_3$.

Wpisanie polecenia z1 = (-1)**(1.0/3) skończy się komunikatem o błędzie: negative number cannot be raised to a fractional power. Musimy użyć liczb zespolonych:

Pozostałe pierwiastki trzeciego stopnia z liczby -1 znajdziemy tak: $z_2=z_1^2,\,\,z_3=z_1^3$

Ukryj

Funkcje matematyczne

Zazwyczaj w obliczanym wyrażeniu chcemy skorzystać z funkcji matematycznych oraz z wyników wcześniej wykonanych obliczeń.
Wyniki wcześniejszych obliczeń możemy zapamiętać w zmiennych.

Utworzone zmienne możemy wykorzystać w dalszych obliczeniach. Policzmy $(11^2+8^3)^{11^2+8^3}$

Powyżej jest tylko pierwszych 80 cyfr wyniku, pełny wynik ma 1774 cyfry.

Pełny wynik

Ukryj

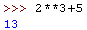
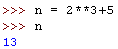
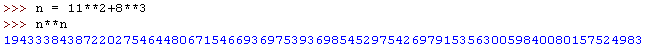
Funkcje matematyczne znajdują się w pakiecie math. Przed użyciem musimy je zaimportować. Są dwa sposoby importu:

Pierwszy sposób wymaga późniejszego używania pełnych nazw funkcji i stałych np. math.sin(math.pi). W zamian, możemy poleceniem dir(math) wyświetlić listę wszystkich funkcji i stałych.
Po imporcie drugim sposobem możemy używać krótkich nazw sin(radians(30)).

Możemy wpisać oba polecenia importu, uzyskamy wtedy komplet zalet: krótkie nazwy i listę obiektów matematycznych.

Policzmy $\sqrt{2^2+3^2}\cdot e^{2^2+3^2}\sin(2^2+3^2)$

Pętle

Do dyspozycji mamy dwa rodzaje pętli:

while warunek – pętla wykonywana jest dopóki spełniony jest warunek
for i in lista – pętla wykonywana jest dla wszystkich liczb $i$ należących do listy

Korzystając z pętli while, obliczymy przybliżoną wartość sumy szeregu $\sum \limits_{n=1}^\infty \frac{1}{n^2}$

Zsumujemy skończoną ilość wyrazów, obliczenia przerwiemy gdy kolejny obliczony wyraz będzie mały.

suma = 0
n = 1
epsilon = 0.00000001
wyraz = 1
while wyraz > epsilon:
  suma = suma + wyraz
  n = n + 1;
  wyraz = 1.0/(n*n)
print(suma) ⇒ 1.64483406185

Czy wynik jest poprawny

Zaawansowanymi metodami analizy matematycznej (szeregi Fouriera) można wykazać, że: $\sum \limits_{n=1}^\infty \frac{1}{n^2}=\frac{\pi^2}{6}$

wynik prawie dokładny = 1.6449340668482264
nasze przybliżenie = 1.64483406185
różnica 1 - 2 = 0.000100005000161

Ukryj

Pętle for wykorzystamy do obliczenia i wyświetlenia wartości silni.

n = 30
wynik = 1
for k in range(1, n+1):
  wynik = wynik*k
  print(k, "! = ", wynik, sep = '')

Funkcja range(a,b) (liczby $a$ i $b$ są całkowite) zwraca listę liczb $[a,\,a + 1,\,\ldots,\,b - 1]$

Wyniki

1! = 1
2! = 2
3! = 6
4! = 24
5! = 120
6! = 720
...
25! = 15511210043330985984000000
26! = 403291461126605635584000000
27! = 10888869450418352160768000000
28! = 304888344611713860501504000000
29! = 8841761993739701954543616000000
30! = 265252859812191058636308480000000

Ukryj

Rysunki dwuwymiarowe

Rysowanie wykresów wymaga zaimportowania pakietu pylab. Pakiet ten nie jest częścią standardu, zatem wymaga dodatkowej instalcji. Opis intalacji można znaleźć na stronie https://www.techwalla.com/articles/how-to-install-pylab-on-python. Podstawowym poleceniem rysującym jest plot. Polecenie to wymaga podania dwóch list (ciagów) liczb tej samej długości. Pierwsza lista zawiera wpółrzędne $x$ rysowanych punktów, druga współrzędne $y$.

We przykładach zakładam, że pakiet pylab jest już zaimportowany poleceniem from pylab import *.

Łamana – wykres funkcji $y=1-|x|$

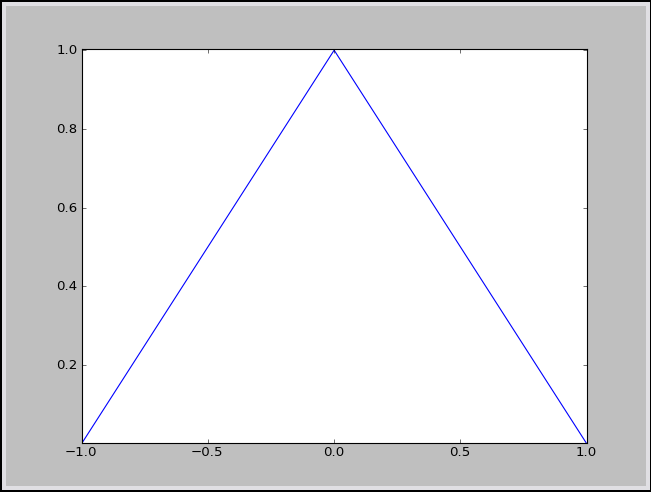Kod
```
x = [-1,0,1]
y = [0,1,0]
plot(x,y)
show()
```
Ukryj

Wykresy funkcji $\sin(x)$ i $\cos(x)$ na jednym rysunku.

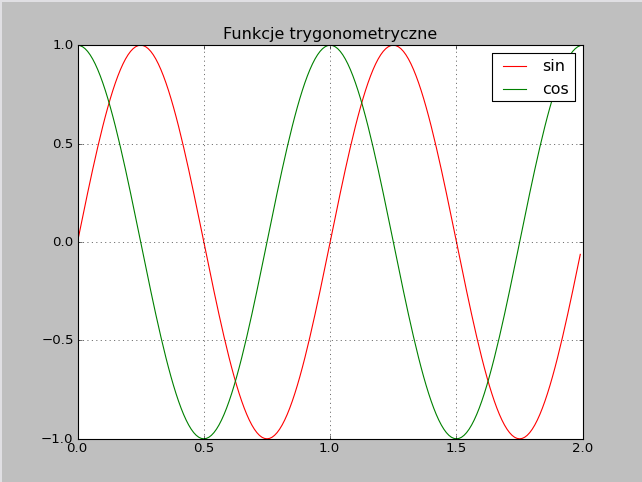Kod

x = arange(0,2,0.01)
#funkcja arange(a,b,krok) tworzy ciąg liczb:
#a, a+krok, a+2*krok, ...
#ostatnia liczba w ciągu jest ≤ b
y1 = sin(2*pi*x)
y2 = cos(2*pi*x)
plot(x,y1,'r',x,y2,'g')
#powyższe polecenie rysuje dwa wykresy
#parametry 'r'('red') i 'g' wyznaczają kolor
legend(('sin','cos'))
title('Funkcje trygonometryczne')
show()

Ukryj

Współrzędne biegunowe – spirala Archimedesa $r=\phi$

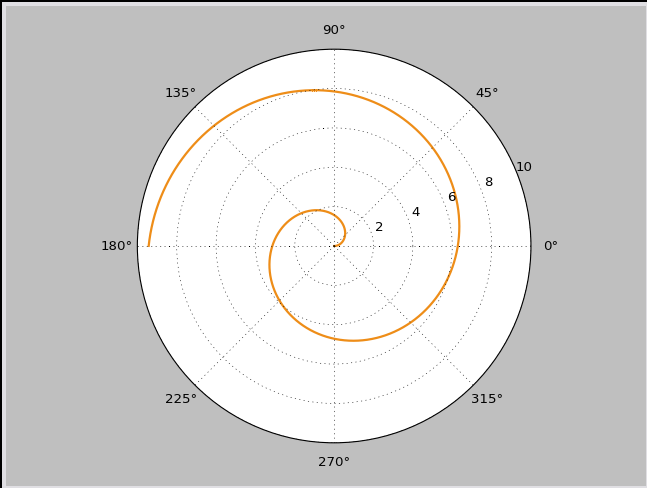Kod

fi = arange(0,3*pi,0.001)
r = fi
polar(fi,r,color="#ee8d18",lw=2)
#funkcja rysuje we współrzędnych biegunowych
#lw = line width
show()

Ukryj

Zadania

Każde z zadań można rozwiązać na wiele sposobów. Kliknięcie w przycisk Kod i wynik pozwala zobaczyć jeden z tych sposobów i poprawny wynik. Prezentowane rozwiązania są kompletne, tzn. zawierają wszystkie konieczne polecenia importu.

Oblicz symbol Newtona $\binom{33}{17}$.

Kod i wynik

from math import *
factorial(33)/(factorial(17)*factorial(16))

$1166803110$

Ukryj

Oblicz pole trójkąta o bokach $2,\,3,\,4$.

Kod i wynik

Stosujemy wzór Herona.

from math import *
p = (2 + 3 + 4)/2.0
sqrt(p*(p-2)*(p-3)*(p-4))

$2.9047375096555625$

Ukryj

Definicja ciągu Fibonacciego: $F_1=1,\,F_2=1,\,\dots,F_n=F_{n-2}+F_{n-1}\,\,dla\,\,n>2$. Oblicz $F_{50}$.

Kod i wynik

a = 1
b = 1
for n in range(48):
  b,a = a+b,b
b

$12586269025$

Ukryj

$\sum\limits_{i=1}^\infty \frac{1}{2^i}=1$ Jak duże musi być $n$, by $\sum\limits_{i=1}^n \frac{1}{2^i} > 0.99999$?

Kod i wynik

suma = 0
i = 1
while suma <= 0.99999:
  suma = suma + 2**(-i)
  i = i + 1
i - 1

$17$

Ukryj

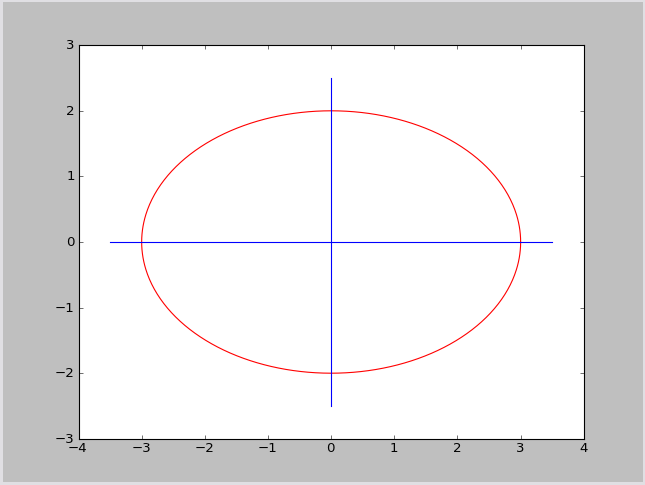
Narysuj kolorem czerwonym elipsę $(\frac{x}{3})^2+(\frac{y}{2})^2=1$ oraz kolorem niebieskim jej osie symetrii.

Kod i wynik

from pylab import *
t = arange(0,2*pi,0.01)
x = 3*cos(t)
y = 2*sin(t)
x2 = [0,0]
y2 = [-2.5,2.5]
x3 = [-3.5,3.5]
y3 = [0,0]
plot(x,y,"r",x2,y2,"b",x3,y3,"b")
show()

Ukryj