Załózmy, że rozwiązujemy równanie postaci: $f(x)=0\,\,\,a\le x \le b$
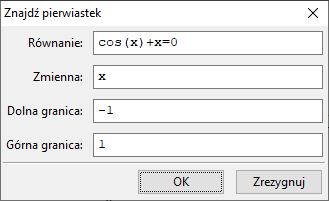
Maxima wykorzystuje metodę bisekcji, która wymaga by $f(a)\cdot f(b)\le 0$. W konsekwencji, Maxima odmawia współpracy, jeżeli $f(a)\cdot f(b) \gt 0$, również wtedy
gdy w przedziale $[a,b]$ są rozwiązania równania.
⇒
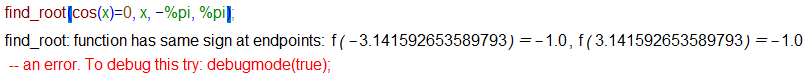
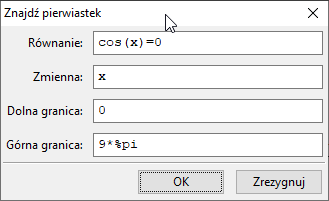
Jeżeli we wskazanym przedziale jest więcej rozwiązań, to
Maxima znajduje tylko jedno z nich.
⇒
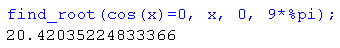
Ukryj uwagi
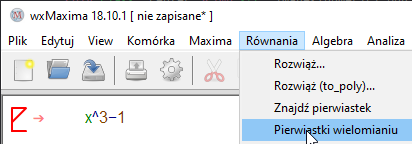
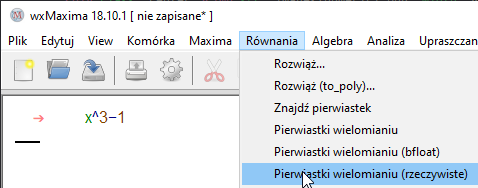
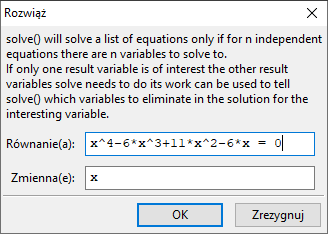
Pierwiastki wielomianu, nie otwiera się okienko kreatora. Wielomian należy wpisać w głównym oknie programu wcześniej.
⇒

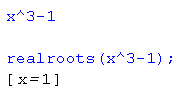
Pierwiastki wielomianu rzeczywiste, też nie otwiera się okna kreatora. Zgodnie z obietnicą, obliczane są tylko pierwiastki rzeczywiste.
⇒
Zadania
Zadania można rozwiązać na wiele sposobów. Kliknięcie w przycisk Rozwiązanie pozwala zobaczyć jeden z tych sposobów.
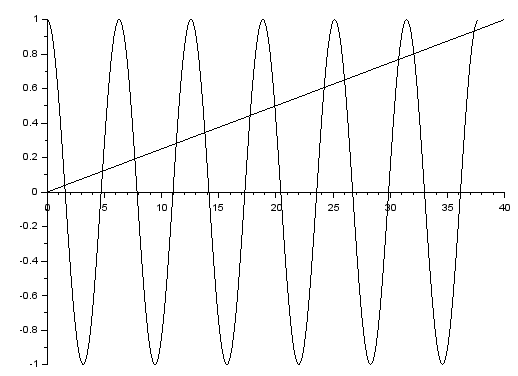
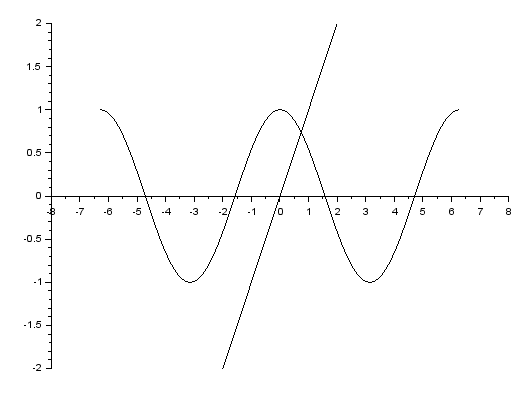
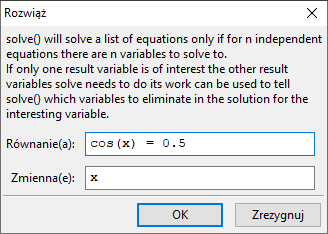
Poniżej – na jednym rysunku – znajdują się wykresy funkcji $y=\cos(x)$ i $y=\frac{1}{40}\cdot x$. Znajdź dwa różne rozwiązania równania $\frac{x}{40}=\cos(x)$.
Rozwiązanie
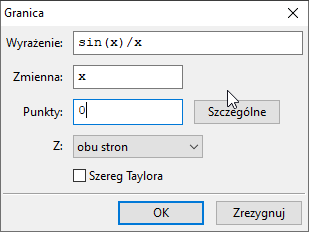
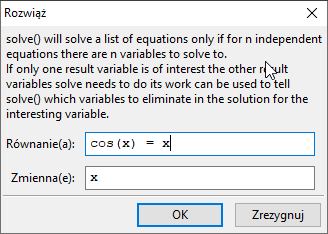
Musimy wybrać rozwiązywanie numeryczne. Kierując sie wykresem, wyznaczamy dwa przedziały $[a,b]$ oraz $[c,d]$ takie, że $f(a)\cdot f(b)\le 0$ oraz $f(c)\cdot f(d)\le 0$, gdzie
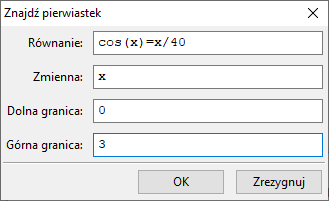
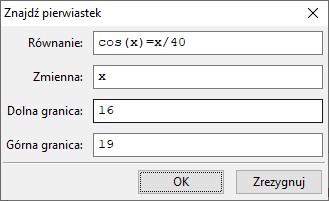
$f(x)=cos(x)-\frac{x}{40}$. Np. $a = 0,\, b = 3,\, c = 16,\, d = 19$. Wykonujemy dwukrotnie polecenie
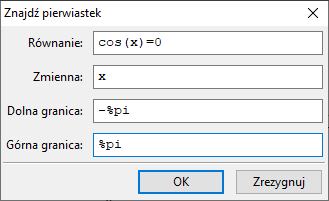
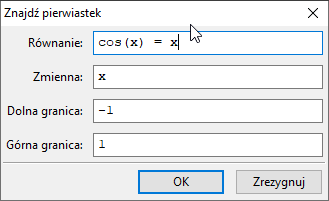
Równania ⇒ Znajdź pierwiastek:
Dostajemy rozwiązania $1.532475071451161$ i $17.7382096279117$.
Ukryj rozwiązanie
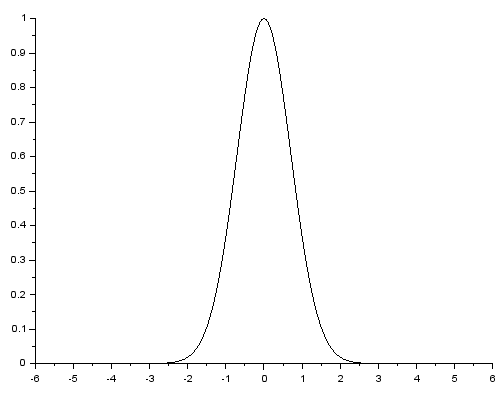
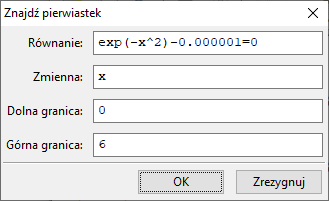
Poniżej znajduje sie wykres funkcji $f(x)=e^{-x^2}$.
Czy $f(4)\lt 0,000001$?
Rozwiązanie
Niech $g(x)=f(x)-0,000001$. Poszukajmy rozwiązań równania $g(x) = 0$ na przedziale $[0,6]$.
Rozwiązanie istnieje i jest równe $3.716922188849838\lt 4$. Funkcja $g$ jest dla $x\ge 0$ malejąca, zatem $g(4) \lt 0$ ⇒ $f(4)\lt 0,000001$.
Ukryj rozwiązanie
Krzywe dwuwymiarowe
Krzywe o równaniu $y = f(x)$
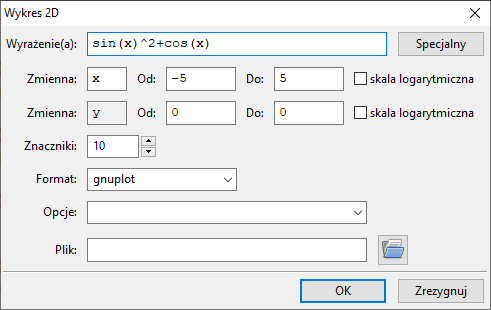
Najprostszy sposób rysowania krzywych dwuwymiarowych, to wybranie z menu pozycji: Wykres ⇒ Wykres2D
Kreator wygeneruje takie polecenie:
plot2d([sin(x)^2 + cos(x)], [x, -5, 5], [plot_format, gnuplot])$
Warto wybrać format gnuplot i nie podawać zakresu zmiennej $y$.
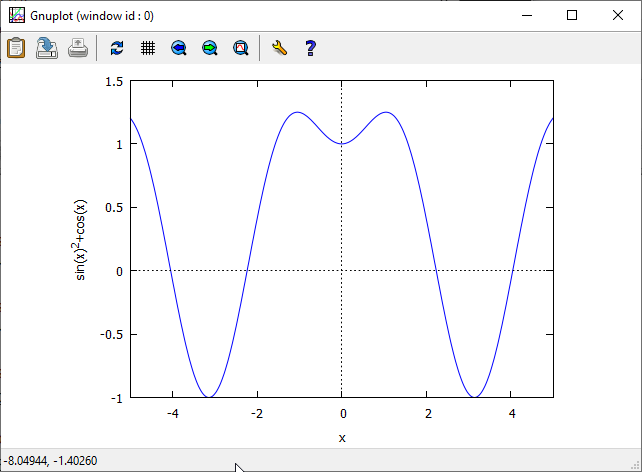
Program rysujący sam ustalił zakres zmiennej $y$, użytkownik programu mógłby wybrać zupełnie źle.
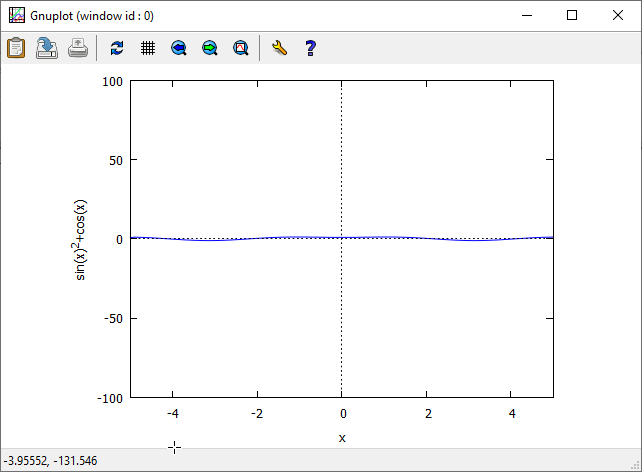
Przykłady złych wyborów
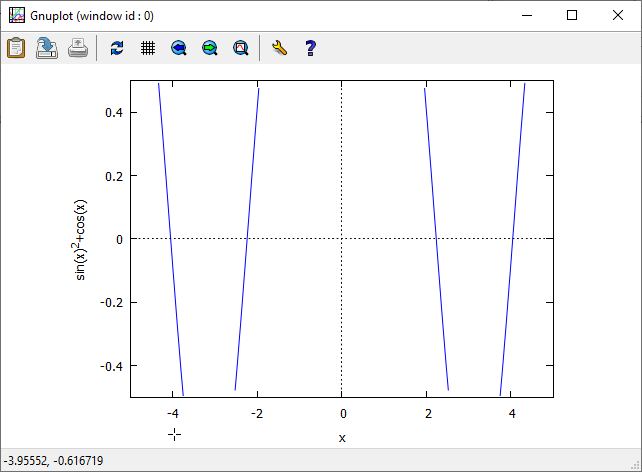
Wykres funkcji $y={sin(x)}^2+cos(x)$.
$-100\le y\le 100$
$-0,5\le y\le 0,5$
Ukryj przykłady
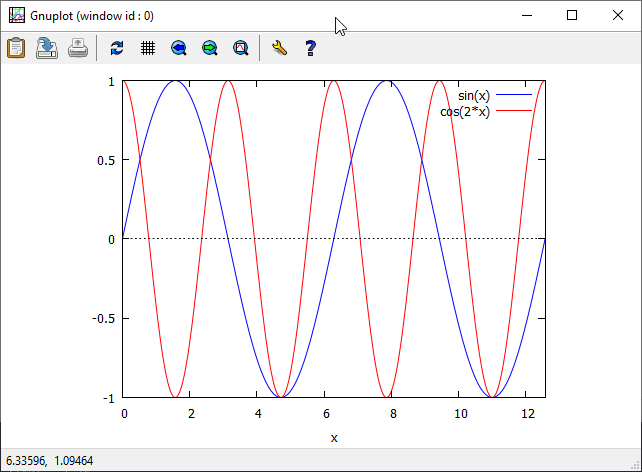
Użycie kreatora ma jedną poważną wadę – nie można umieścić wykresów kilku funkcji na jednym rysunku. Polecenie rysujące kilka wykresów musimy napisać:
plot2d([sin(x), cos(2*x)], [x, 0, 4*%pi], [plot_format, gnuplot]);
Krzywe parametryczne
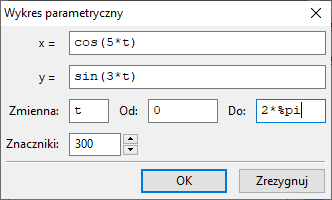
Ponownie wybieramy z menu pozycję Wykres ⇒ Wykres2D, klikamy w przycisk Specjalne i z menu podręcznego wybieramy Parametryczny.
Warto wybrać format gnuplot i nie podawać zakresu ani zmiennej $x$, ani zmiennej $y$.
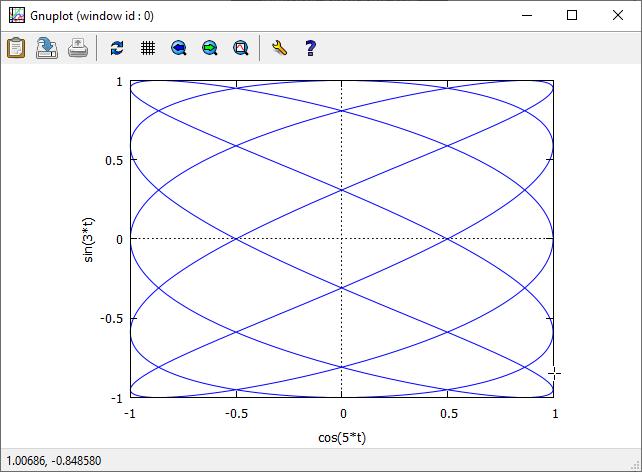
Otrzymana krzywa jest szczególnym przypadkiem tzw. krzywych Lissajous.
Program rysujący sam ustalił zakresy zmiennych $x$ i $y$.
W aktualnej wersji wxMaximy (21.05.2) kreator generuje błędne polecenie rysowania:
plot2d([$, 'parametric, cos(5*t), sin(3*t), [t, 0, 2*%pi]], [nticks, 300], [x, -5, 5], [plot_format, gnuplot],)$
trzeba je poprawić (generowane polecenie
ma niekiedy inną postać, ale zawsze jest błędne):
plot2d([[parametric, cos(5*t), sin(3*t), [t, 0, 2*%pi]]], [nticks, 300], [plot_format, gnuplot])$
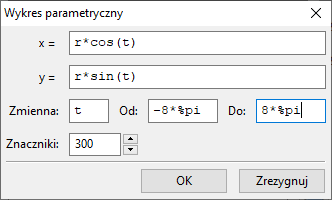
W kolejnym przykładzie krzywej parametrycznej (tzw. krzywa motyla), pewne skomplikowane wyrażenie pojawia się we wzorze na $x$ i we wzorze na $y$. Aby uniknąć dwukrotnego wpisywania tego
wyrażenia, możemy je zdefiniować w oknie graficznym Maximy.
Wyrażenie to zostało nazwane $r$, można z niego korzystać w okienku Parametryczny:
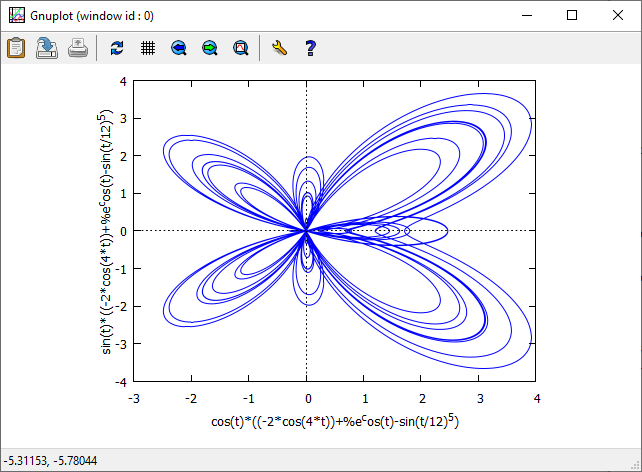
Wygenerowane przez kreator polecenie wygląda (po korekcie) tak:
plot2d([[parametric, r*sin(t), r*cos(t), [t, -8*%pi, 8*%pi]]], [nticks, 2000])$
A sama krzywa tak:
Zadania
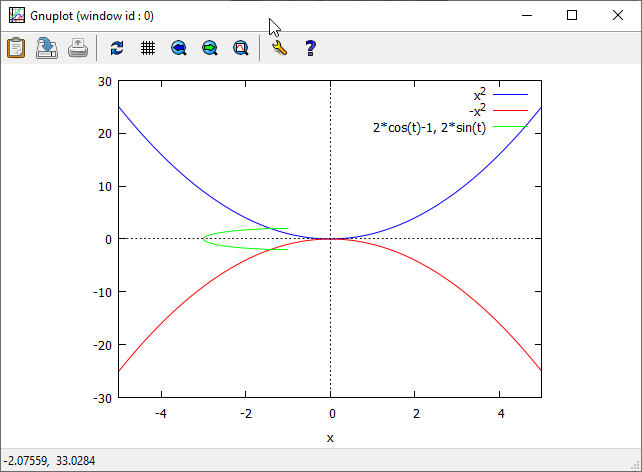
Narysuj na jednym rysunku trzy krzywe:
- parabolę o równaniu $y=x^2$,
- parabolę o równaniu $y=-x^2$,
- lewą połowę okręgu opisanego parametrycznie $x=2\cdot \cos(t)-1\,\,\,y=2\cdot \sin(t)$.
Rozwiązanie
Chyba najprostszym rozwiązaniem jest napisanie polecenia:
plot2d([x^2, -x^2, [parametric, 2*cos(t) - 1, 2*sin(t), [t, %pi/2, 3*%pi/2]]],[x, -5, 5])$
Ukryj rozwiązanie
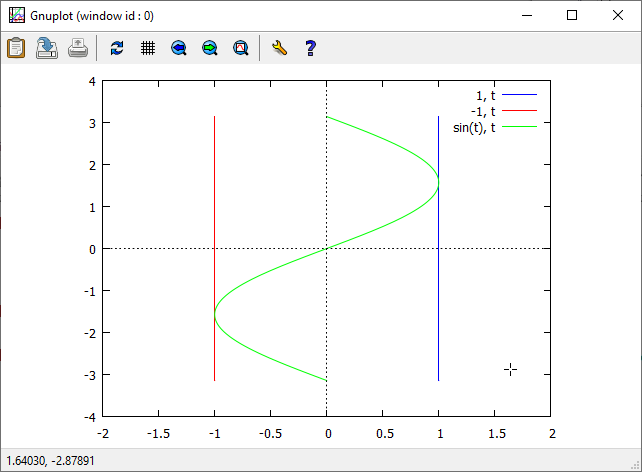
Narysuj na jednym rysunku trzy krzywe:
- sinusoidę o równaniu $x=\sin(y)$,
- prostą o równaniu $x=1$,
- prostą o równaniu $x=-1$.
Rozwiązanie
Wszystkie krzywe opiszemy parametrycznie. Ponownie napiszemy polecenie:
plot2d([[parametric, 1, t, [t,-%pi,%pi]], [parametric, -1, t, [t,-%pi,%pi]], [parametric, sin(t), t, [t,-%pi,%pi]]], [x,-2,2])$
Ukryj rozwiązanie
Elementy programowania
Własne funkcje
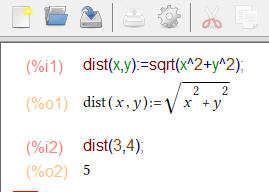
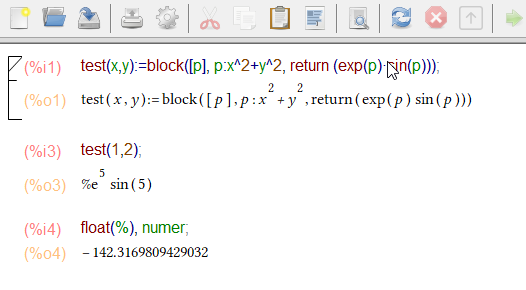
Używanie własnych funkcji ułatwia korzystanie z Maximy. Przypuśćmy, że będziemy wielokrotnie obliczać odległość punktu $(x,y)$ od początku układu. Definiujemy funkcję:
Jeżeli chcemy wewnątrz funkcji użyć dodatkowych zmiennych do przechowania wyników pomocniczych obliczeń, to definicja funkcji staje się bardziej skomplikowana:
Wiersz (%i4) wygenerowałem wykonując poniższe polecenie:
Tak zdefiniowane funkcje nie istnieją po zamknięciu i ponownym uruchomieniu programu Maxima (wxMaxima). Polecenia: Maxima ⇒ Restart Maxima i
Maxima ⇒ Wyczyść pamięć również usuwają funkcje.
Jeżeli chcemy korzystać z funkcji wielokrotnie, to musimy ją zapisać do pliku: Plik ⇒ Zapisz i w razie potrzeby odczytać z pliku: Plik ⇒ Otwórz.
Napisz funkcję $\text{isTriangle}(a,b,c)$, która zwraca wartość logiczną true jeżeli istnieje trójkąt o długościach bokach $a$, $b$ i $c$, a wartość logiczną false
jeśli taki trójkąt nie istnieje.
Rozwiązanie
Pętla for
Pętla for wymusza wykonanie pewnego kodu dla wielu wartości pewnej zmiennej nazywanej zmienną sterującą.
W powyższym przykładzie wpierw definiowana została funkcja $F(n)$ obliczająca tzw.
liczby Fermata.
Następnie, za pomocą pętli
for wypisane zostało siedem liczb Fermata wraz z informacją czy są one pierwsze. Zmienna sterująca oznaczona jest literą $i$, nie jest to przypadek –
wiekszość zmiennych sterujących w pisanych na świecie pętlach
for jest oznaczana literą $i$.
Funkcja primep
Funkcja $primep(n)$ jest dość tajemnicza:
- jeśli $primep(n) = false$, to liczba $n$ jest na pewno złożona,
- jeśli $primep(n) = true$ oraz $n\lt 341550071728321$, to liczba $n$ jest na pewno pierwsza,
- jeśli $primep(n) = true$ oraz $n\ge 341550071728321$, to liczba $n$ jest pierwsza z prawdopodobieństwem $1-10^{-15}$.
Ukryj wyjaśnienia
Ogólna postać pętli for jest następująca:
for zm_ster:wart_pocz [step krok] «kontrola» do «kod_do_wykonania»
Fragment step krok jest nieobowiązkowy, liczba krok decyduje o ile zmienia się wartość zmiennej sterującej, liczba ta może być ujemna, może być ułamkowa. Domyślnie
$\text{krok}=1$.
Fragment «kontrola» może mieć kilka postaci:
thru wart_konc, wartość zmiennej sterującej nie przekroczy wart_konc,while warunek, wykonywanie pętli zakończy się gdy warunek nie będzie spełniony
for i:1 while (i <= 5) do print(i)
unless warunek, wykonywanie pętli zakończy się gdy warunek będzie spełniony
for i:1 unless (i > 5) do print(i)
Korzystając z pętli for wypisz – w kolejności malejącej wszystkie liczby nieparzyste z przedziału $[100,200]$ i ich kwadraty.
Rozwiązanie
Tablice
Możliwości pętli for znacznie wzrastają gdy korzystamy z tablic. Tablice w Maximie mogą być wielomiarowe, będziemy korzystać tylko z tablic dwuwymiarowych i jednowymiarowych.
Warto pamiętać, że indeksowanie elementów w tablicy zaczyna sie od zera.
Tworzenie tablic:
- tablica jednowymiarowa
array(nazwa, index_ostatniego_elementu)
- tablica dwuwymiarowa
array(nazwa, index_ostatniego_wiersza, index_ostatniego_elementu_w_wierszu)
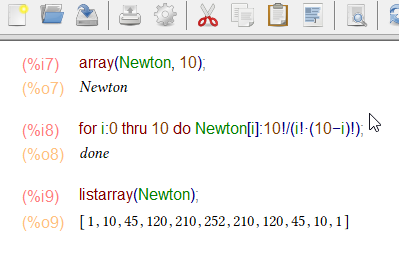
Tworzenie jednowymiarowej tablicy o nazwie Newton, zawierającej symbole Newtona $\binom{10}{0}\dots \binom{10}{10}$.
Obliczenie sumy liczb z tablicy Newton oraz wyznaczenie liczby największej i najmniejszej. Jeżeli w pętli for w kodzie po słowie do chcemy wykonać kilka
instrukcji, to rozdzielamy je przecinkami i całość ograniczami nawiasami:
… do (instrukcja1, instrukcja2, ...)
Utworzenie dwuwymiarowej tablicy o 2 wierszach i 21 kolumnach. Do pierwszego wiersza wpiszemy pierwsze 21 wyrazów ciągu Fibonacciego $f_0=1,\,f_1=1,\,f_n=f_{n-2}+f_{n-1}$ dla $n\ge 2$, w drugim wierszu na pozycji
o indeksie $n\, (n\gt 1)$ wpiszemy $\frac{f_n}{f_{n-1}\cdot\phi}$ gdzie $\phi=\frac{1+\sqrt 5}{2}$ jest tzw. złotą liczbą.
array(fibo, 1, 20)
fibo[0, 0]:1
fibo[0, 1]:1
for i:2 thru 20 do
fibo[0, i]:fibo[0, i - 2] + fibo[0, i - 1]
gold:(1 + sqrt(5))/2
for i:1 thru 20
do fibo[1, i]:fibo[0, i]/(fibo[0, i - 1]*gold)
for i:0 thru 20
do print(fibo[0, i], " ", float(fibo[1, i]))
Ostatnie wiersze na ekranie wyglądają tak:
Zadania
Oblicz sumę $\sum_{n=1}^{100}n^3$.
Rozwiązanie
suma:0
for i:1 thru 100 do suma:suma + i^3
print(suma) ⇒ 25502500
Ukryj rozwiązanie
Rozważmy prostokąty o bokach $a$ i $b$ będących liczbami nieparzystymi, spełniającymi warunek $a+b=100$. Jaka jest największa wartość pola tych prostokątów?
Rozwiązanie
M:0
for a:1 step 2 thru 100 do (pole:a*(100 - a), M:max(M, pole))
print(M) ⇒ 2499
Ukryj rozwiązanie
Ile składników szeregu geometrycznego $\sum_{i=1}^\infty\frac{1}{2^i}$ trzeba zsumować aby otrzymana suma częściowa była większa od $0,99999999$?
Rozwiązanie
suma:0
licznik:0
for i:1 while (suma <= 0.99999999) do (suma:suma + 1/2^i, licznik:licznik+1)
print(licznik) ⇒ 27
Ukryj rozwiązanie
Napisz funkcję, która dla liczby $n$ zwraca liczbę liczb pierwszych nie przekraczających $n$.
Rozwiązanie
primes(n):=block([p], p:0, for i:2 thru n do if primep(i) then p:p+1, return(p))
Dla kontroli:
primes(3) ⇒ 2
primes(10) ⇒ 4
primes(100) ⇒ 25
Ukryj rozwiązanie
Napisz funkcję, która dla liczby $x$ zwraca odległość od najbliższej liczby całkowitej podzielnej przez 10.
Przydatne funkcje:
floor(x) zwraca przybliżenie całkowite liczby $x$ z dołu,ceiling(x) zwraca przybliżenie całkowite liczby $x$ z góry,abs(x) zwraca wartość bezwzględną liczby $x$,mod(n, k) zwraca resztę z dzielenia liczby $n$ przez liczbę $k$
Rozwiązanie
near(x):=block([d], d:10, for i:floor(x) - 10 thru ceiling(x) + 10 do if mod(i, 10) = 0 then d:min(d, abs(i - x)), return(d))
Dla kontroli:
near(3.67) ⇒ 3.67
near(18.76) ⇒ 1.239999999999998
near(-5.67) ⇒ 4.33
Ukryj rozwiązanie



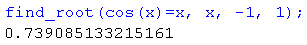
 ⇒
⇒ 
 ⇒
⇒ 
 ⇒
⇒ 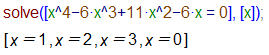
 ⇒
⇒ 
 ⇒
⇒
 ⇒
⇒ 
 ⇒
⇒  Uwagi
Uwagi ⇒
⇒ 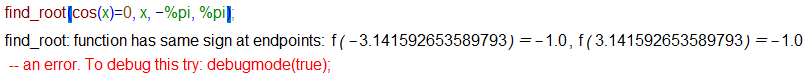
 ⇒
⇒ 
 ⇒
⇒ 
 ⇒
⇒