Arkusze kalkulacyjne

Na krzywej o równaniu $$\frac{(x-2)^2}{4}+y^2=1\,\,(1)$$

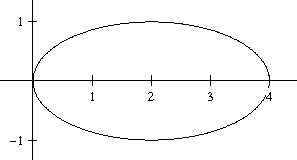chcemy, korzystając z narzędzia Solver, znaleźć jeden z punktów leżących najdalej od początku układu.

Czy wyznaczenie maksimum funkcji $$f(x,y)=x^2+y^2$$ przy ograniczeniach $\begin{cases}0\le x\le 4\\0\le y\le 1\\x^2-4x+4y^2=0\,\,\,\,(2)\end{cases}$da nam rozwiązanie?

Tak

Nie

Brawo!

Wyjaśnienia

Niestety, źle

Wyjaśnienia

Funkcja $f(x,y)=x^2+y^2$ osiąga wartość największą w tym samych punktach co funkcja odległości $d(x,y)=\sqrt{x^2+y^2}$.
Prosta $y=0$ jest osia symetrii dla badanej krzywej (elipsy). Zatem jeden z punktów najdalszych musi leżeć w górnej półpłaszczyźnie $y>0$.
Równania (1) i (2) są równoważne.