Arkusze kalkulacyjne
Excel i Calc
Na odcinku $\overline{AB},\, A=(-1,1),\, B=(3,2)$ wyznaczymy punkty leżące najdalej i najbliżej od początku układu. Najpierw, korzystając z kartki, napiszemy równanie
prostej przechodzącej przez punkty $A,B$, ma ono postać $4\cdot y-x-5=0$. By znaleźć punkt najbliższy i najdalszy, znajdziemy punkty, w których funkcja
$$f(x,y)=x^2+y^2$$ osiąga wartość największą i najmniejszą. Zmiennym $x,y$ przydzielimy komórki A9 i B9. Do komórki C9 wpiszemy formułę
opisującą badaną funkcję, a do komórki D9 formułę opisującą równanie prostej.

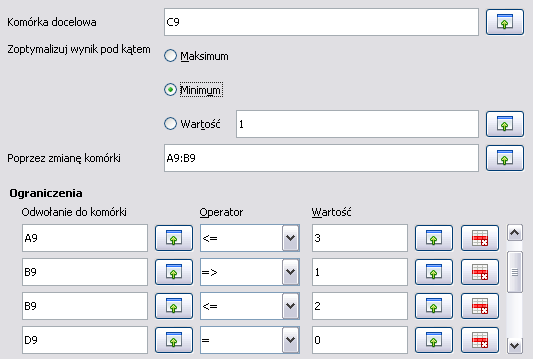 (Na powyższym zrzucie ekranu nie widać warunku $A9\ge -1$.)
(Na powyższym zrzucie ekranu nie widać warunku $A9\ge -1$.)



Uruchamiamy narzędzie Solver:

Zatwierdzamy i w komórkach A9:B9 pojawia się rozwiązanie.

Analogicznie możemy wyznaczyć punkt najdalszy.

Znalezione rozwiązanie pokazuje, że Solver korzysta z algorytmów przybliżonych. Pozwala to rozwiązać znacznie więcej zagadnień, ale w prostych przypadkach może może dawać gorsze rozwiązania. W opisywanym zagadnieniu wystarczy naszkicować rysunek, by zobaczyć, że punktem najdalszym jest punkt $(3,2)$.