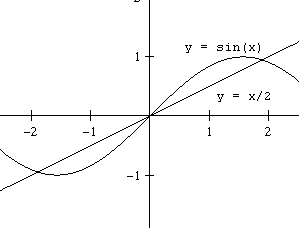Arkusze kalkulacyjne
Excel i Calc
Równanie $$e^{x^2} - 1 - \cos x = 0$$ ma dwa różniące się znakiem pierwiastki. Narzędzie Szukaj wyniku znajduje jeden z nich, dodatni. W tym przypadku
możemy łatwo ustalić wartość drugiego pierwiastka. Taka sytuacja nie jest typowa, jesteśmy zazwyczaj "skazani" na jeden pierwiastek, niekoniecznie ten, który nas interesuje.
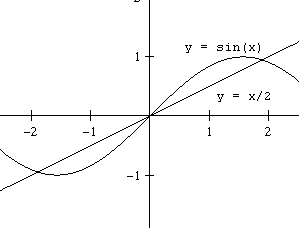 Narzędzie Szukaj wyniku znajdzie oczywiste rozwiązanie $x=0$. Co zrobić jeżeli interesuje nas najmniejsze rozwiązanie dodatnie? Rozpatrzmy nową funkcję,
nazwijmy ją sinus, której wykres częściowo (dla $x\ge0,5$) pokrywa się z wykresem funkcji $\sin(x)$.
Narzędzie Szukaj wyniku znajdzie oczywiste rozwiązanie $x=0$. Co zrobić jeżeli interesuje nas najmniejsze rozwiązanie dodatnie? Rozpatrzmy nową funkcję,
nazwijmy ją sinus, której wykres częściowo (dla $x\ge0,5$) pokrywa się z wykresem funkcji $\sin(x)$.
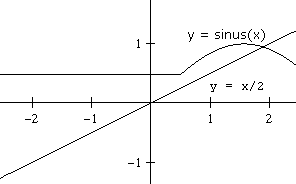
Rozważmy równanie $$\sin(x) = \frac{1}{2}x$$