ciągi zdefiniowane rekurencyjnie | odwzorowanie logistyczne | uruchamianie programów

Chaos deterministyczny

Ciągi zdefiniowane rekurencyjnie

Rozpatrywać będzięmy ciągi różnych typów:

W każdym przypadku dane będzie pewna funkcja $f$ , przy jej pomocy tworzymy ciąg w następujący sposób: (1) wybieramy wyraz „zerowy” $a_0$, kolejne wyrazy obliczamy ze wzoru $a_{n+1} = f(a_n)$.
Uwaga 1: Znany zapewne ciąg Fibonacciego $a_0 = 1,\, a_1 = 1,\, a_n = a_{n-1} + a_{n-2}$ dla $n \ge 2$ można „podciągnąć” pod powyższy schemat traktując go jak ciąg punktów (par liczb): $b_0 = (1; 1),\, b_{n+1} = (b_{n,2};\, b_{n,1} + b_{n,2})$ dla $n \ge 1$.
Uwaga 2: Można uważać iż ciągi zdefiniowane rekurencyjnie opisują zmiany (ewolucję) jakiegoś układu fizycznego, biologicznego, chemicznego itp. Wyraz $a_0$ to stan początkowy, funkcja $f$ to prawo (reguła) wg której zmienia się „świat”: jeśli w chwili obecnej świat jest w stanie $a$, to w chwili „następnej” będzie w stanie $f(a)$.

Dla uproszczenia używał będę zwrotu ciąg punktów niezależnie od tego czy wyrazy ciągu są liczbami, zbiorami czy też „prawdziwymi” punktami.

Jeśli ciąg utworzony w opisany wyżej sposób jest ograniczony, to punkt $a_0$ nazywamy więźniem dla odwzorowania $f$, w przeciwnym razie mówimy iż punkt $a_0$ jest uciekinierem.

(2) Przykłady:

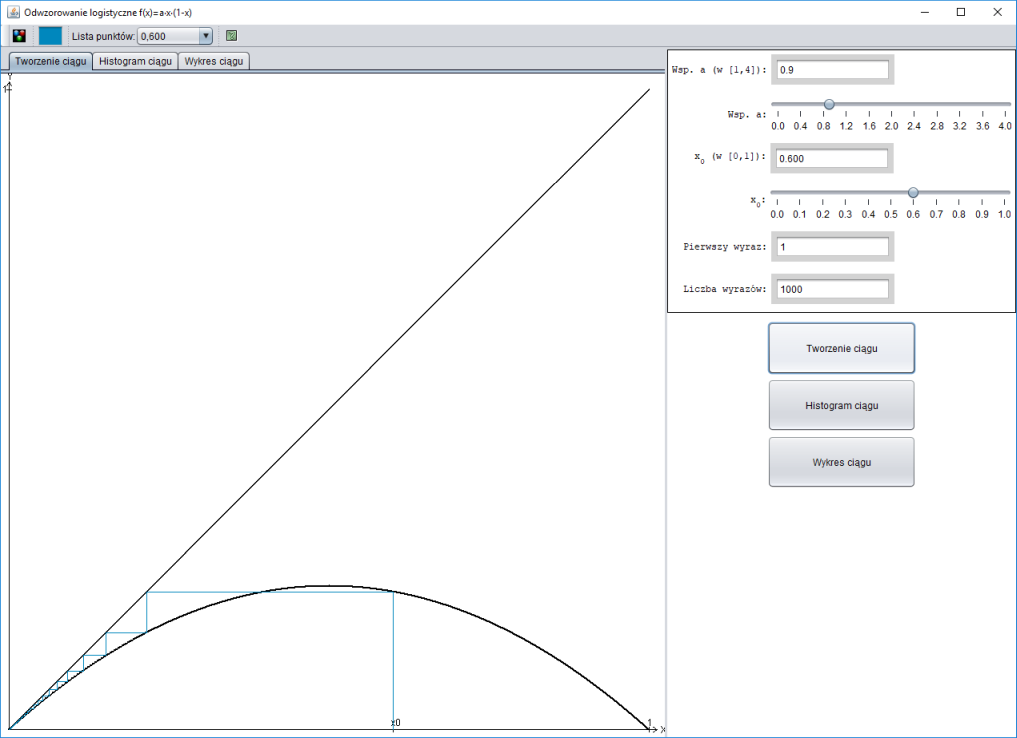
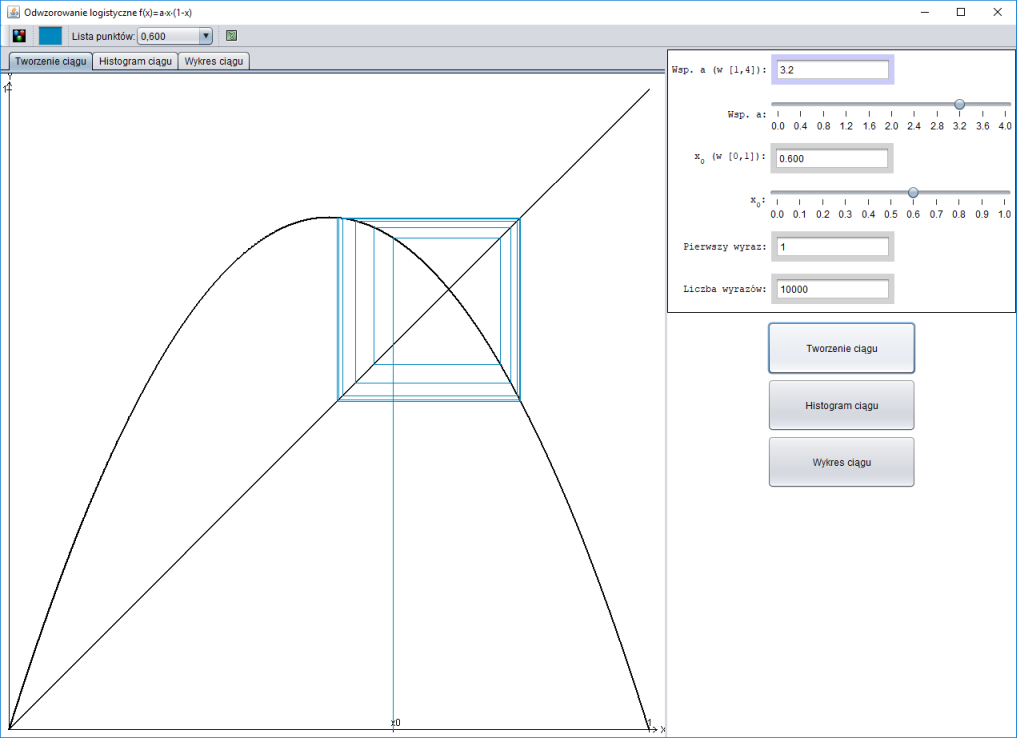
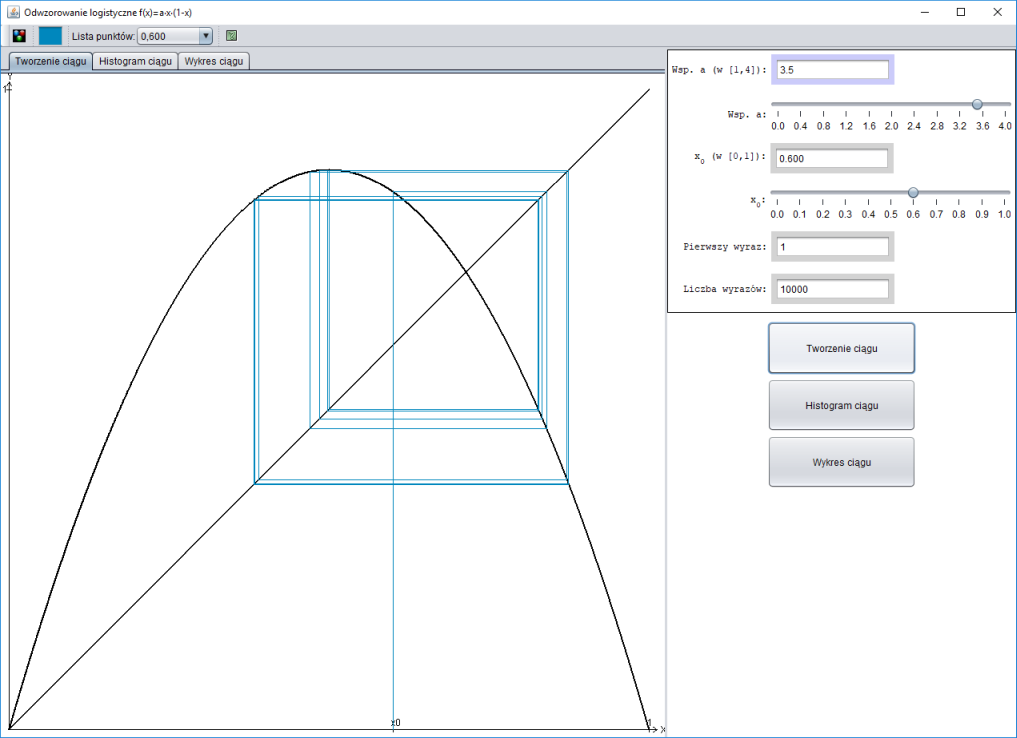
Dla funkcji $f: \mathbb{R} \rightarrow \mathbb{R}$ opisany wyżej ciąg możemy konstruować geometrycznie. Załóżmy, że $f(x) = 3x(1 - x)$.

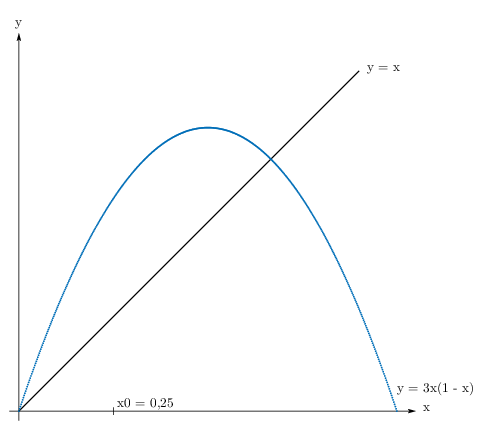
Rysujemy odcinek prostopadły do osi $OX$ od punktu $(x_0;\, 0)$ do przecięcia z wykresem funkcji $f$, punkt przecięcia $A = (x_;\, f(x_0)) = (x_0;\, x_1)$.

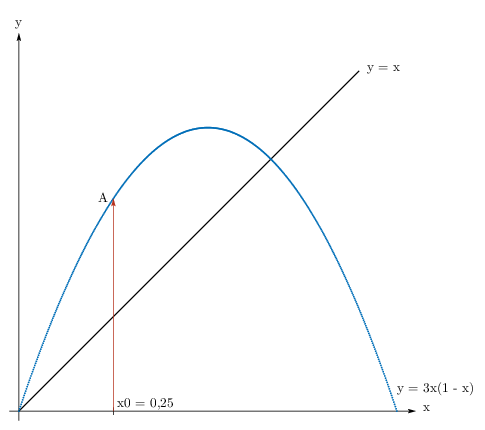
Rysujemy odcinek równoległy do osi $OX$ od punktu $A$ do przecięcia z prostą o równaniu $y = x$, punkt przecięcia $B = (x_1;\, x_1)$.

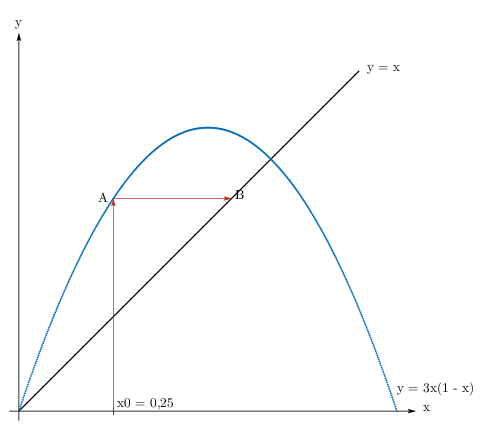
Rysujemy odcinek prostopadły do osi $OX$ od punktu $B$ do przecięcia z osią $OX$, punkt przecięcia to $(0;\, x_1)$.

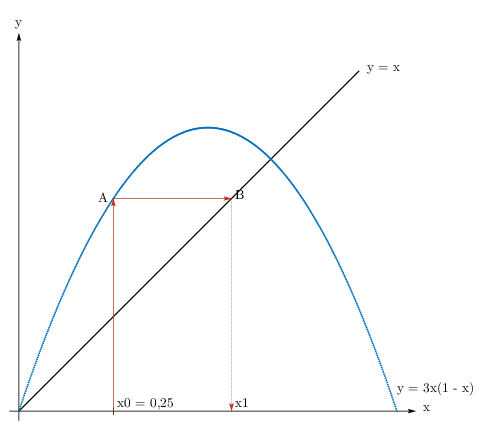
Rysujemy odcinek prostopadły do osi $OX$ od punktu $(0;\, x_1)$ do przecięcia z wykresem funkcji $f$, punkt przecięcia $C = (x_1;\, f(x_1)) = (x_1;\, x_2)$.

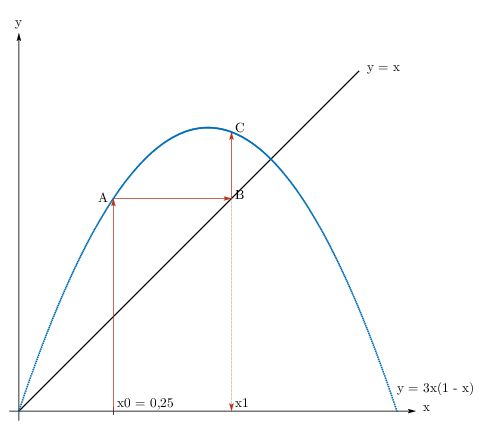
Rysujemy odcinek równoległy do osi $OX$ od punktu $C$ do przecięcia z prostą o równaniu $y = x$, punkt przecięcia $D = (x_2;\, x_2)$.

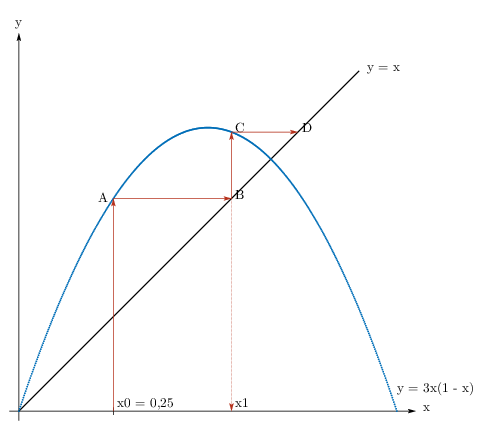
Kontynuujemy rysowanie łamanej.

Zamieszczone dalej rysunki wykonane zostały programem, który nie rysuje linii kropkowanych.

Odwzorowanie logistyczne – przykład chaosu deterministycznego

Odwzorowaniem logistycznym nazywamy funkcję (3) $f_a(x) = ax(1-x),\, 0 \le a \le 4$. Tworzymy (korzystając z procedury (1)) ciąg $(x_n)_{n \ge 0}$. Okazuje się że zachowanie tego ciągu nie zależy od punktu początkowego $x_0$, zależy natomiast bardzo istotnie od wartości współczynnika $a$.
Uwaga: W biologii korzysta się z takiego modelu rozwoju populacji (4):
$p_{n+1} = p_n + c\cdot p_n(1-p_n)$, gdzie $p_n = \frac{P_n}{N}$ jest stosunkiem aktualnej liczebności $P_n$ do maksymalnej liczebności $N$. Jeśli dokonamy podstawień $x_n = \frac{c}{c+1}p_n,\, a = c + 1$, to otrzymamy wzór (3).

Jeżeli $a \lt 1$, to otrzymany ciąg jest szybko zbieżny do zera.

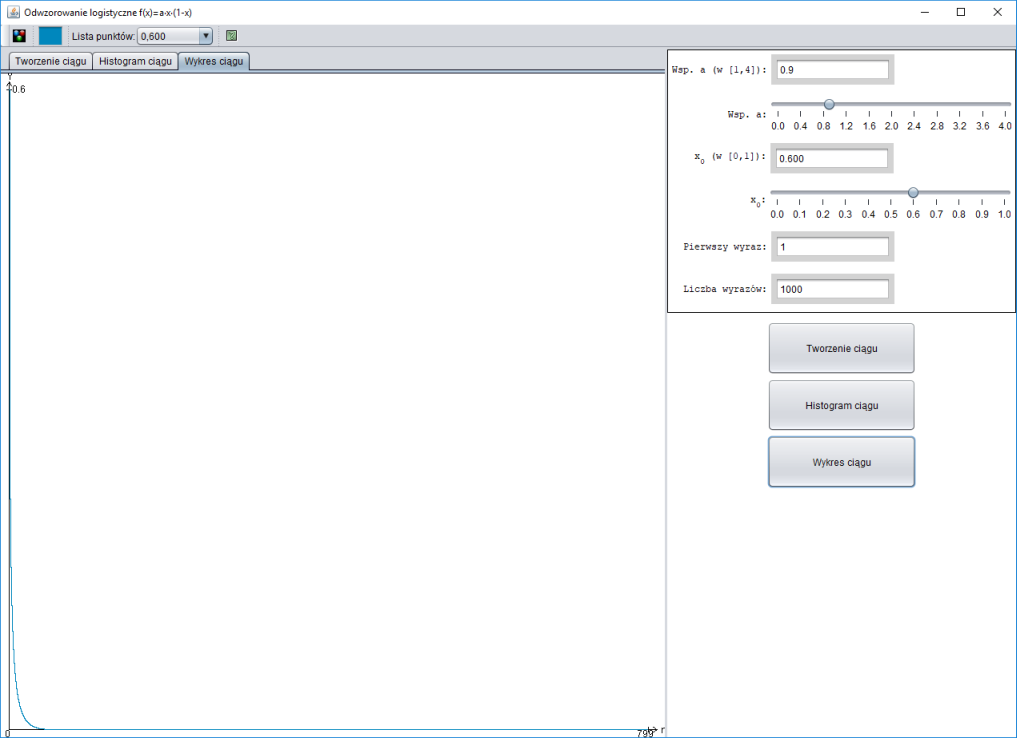
Jeżeli $1 \le a \le 3$, to otrzymany ciąg jest zbieżny do $1 - \frac{1}{a}$ (liczba $1 - \frac{1}{a}$ jest pierwiastkiem równania $f_a(x) = x$).

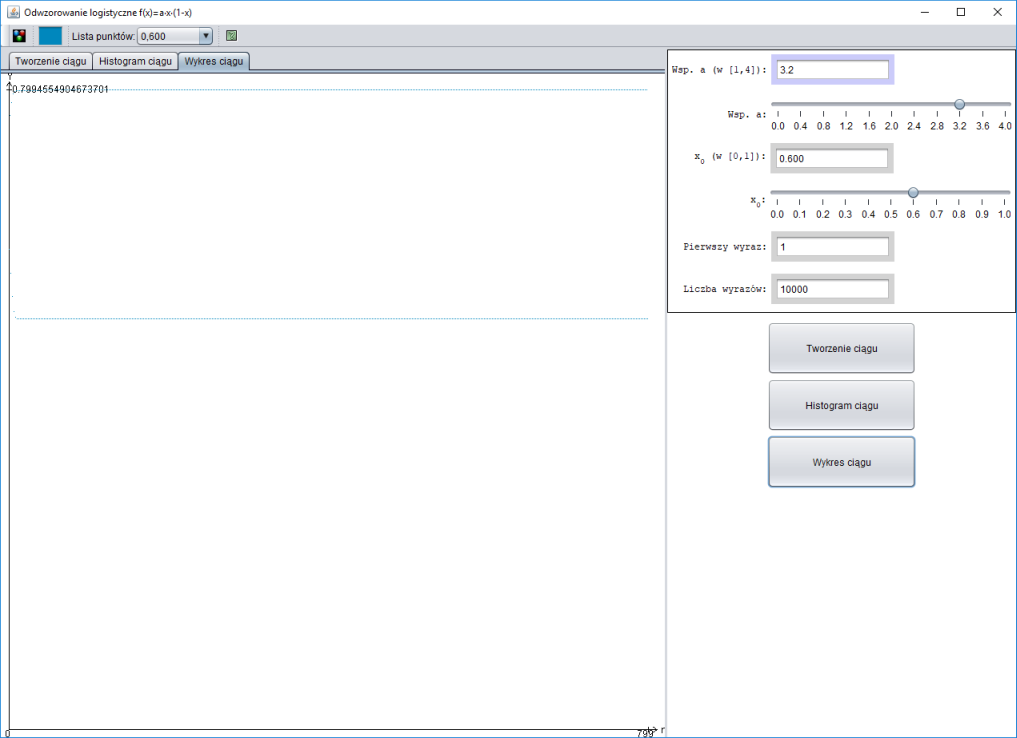
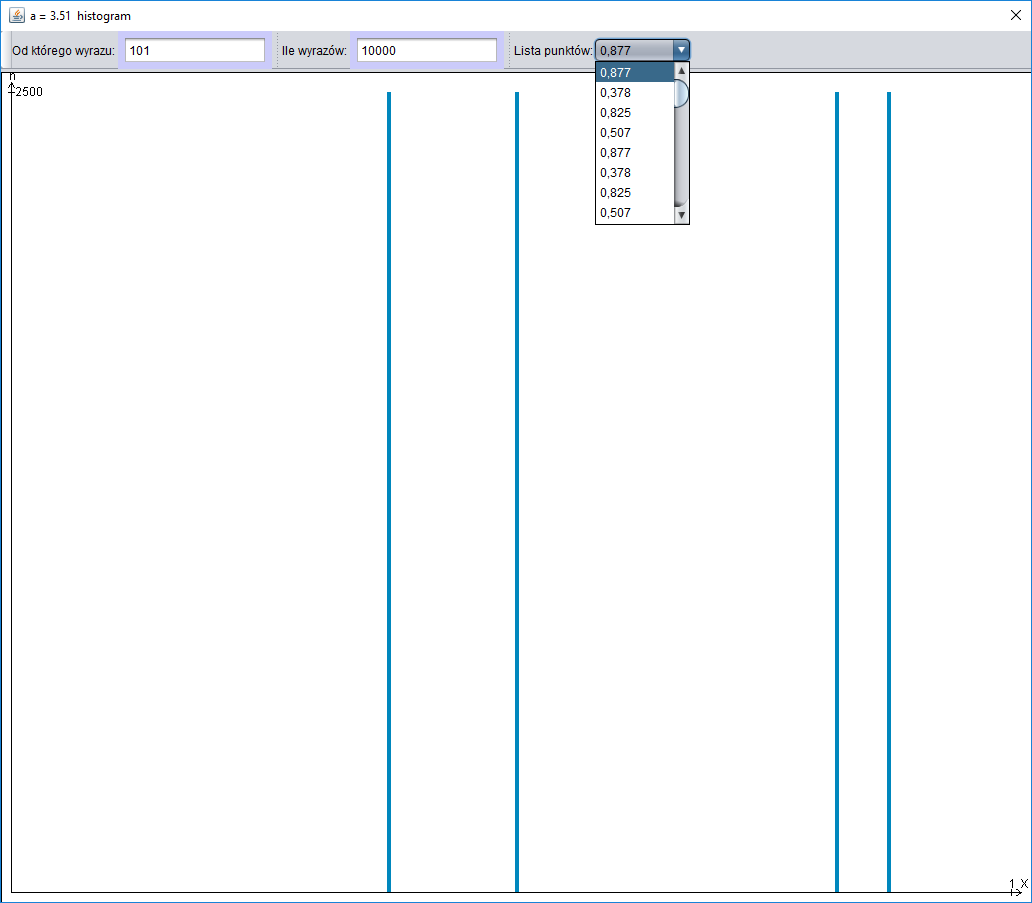
Jeżeli $a \gt 3$, to otrzymujemy ciąg okresowy (okres zależy od $a$) lub całkowicie chaotyczny. Ciąg staje się okresowy po „ustabilizowaniu”, należy zignorować początkowe wyrazy (zazwyczaj wystarczy zignorować około $100$ wyrazów).
Ciąg okresowy o okresie $2$, $a = 3,2$.

Ciąg okresowy o okresie $4$, $a = 3,5$.
Ciąg chaotyczny, $a = 3,9$. Na poprzednich wykresach zaznaczane były tylko punkty $(n,\, x_n)$, poniżej rysowane są również odcinki od $(n,\, x_n)$ do $(n+1,\; x_{n+1})$.

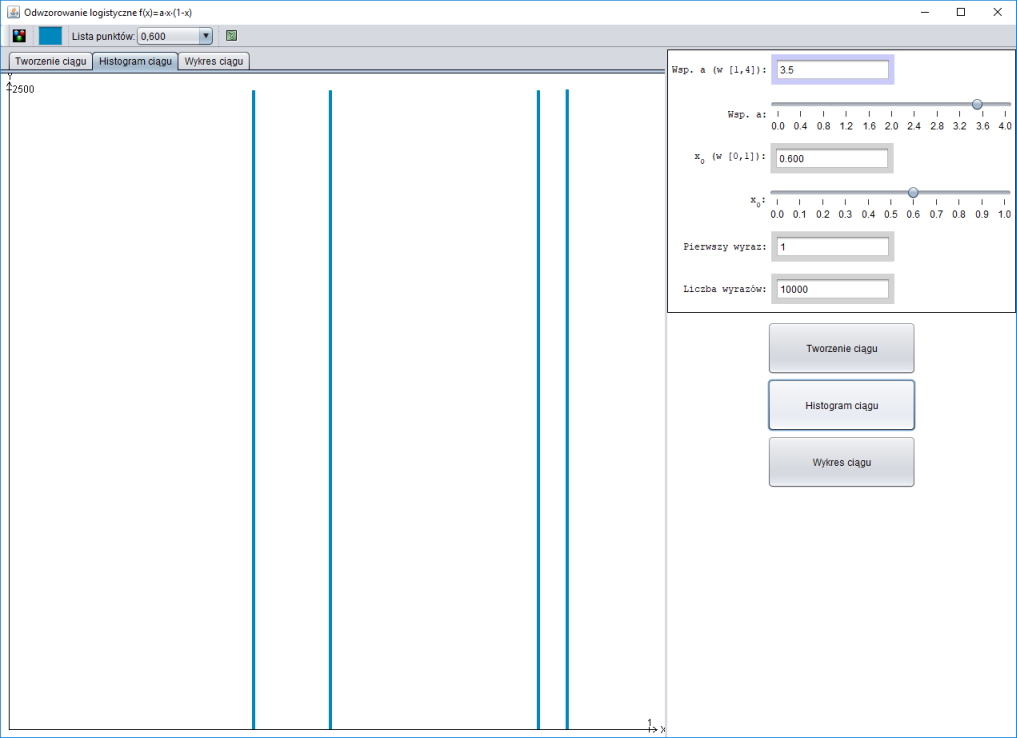
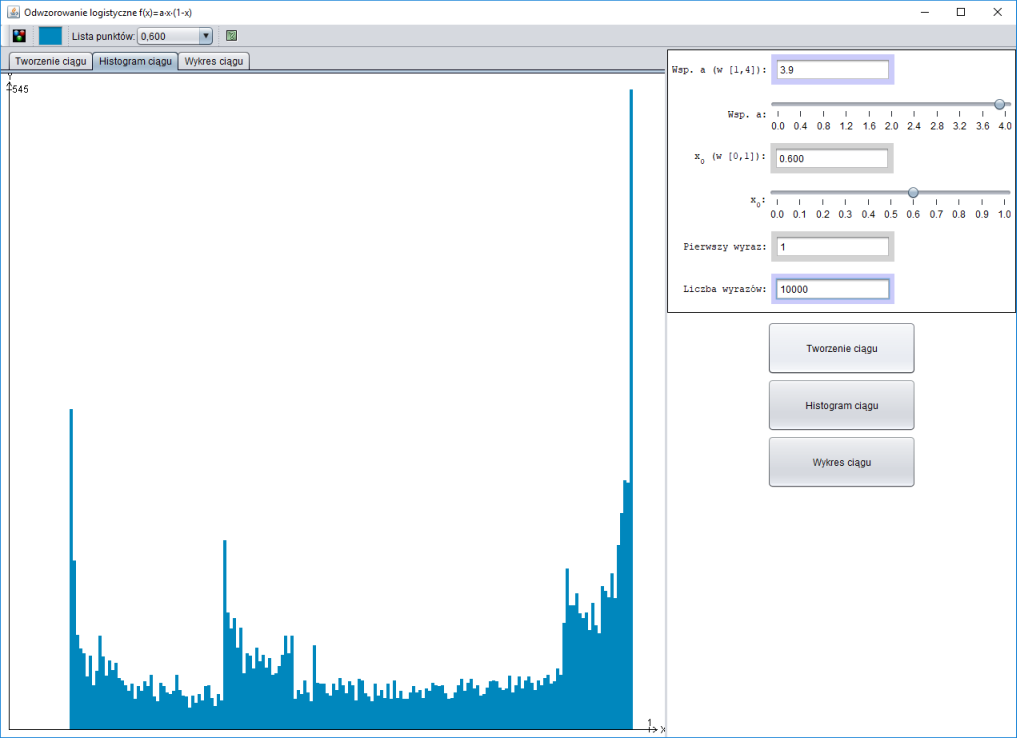
Histogram rysowany jest w następujący sposób, odcinek $[0;\, 1]$ dzielony jest na $200$ rozłącznych odcinków $[0;\, \frac{1}{200}),\, [\frac{1}{200};\, \frac{2}{200}),\ldots,[\frac{199}{200};\, 1]$, na osi $OY$ zaznaczana jest ilość punktów znajdujących się w tym odcinku.

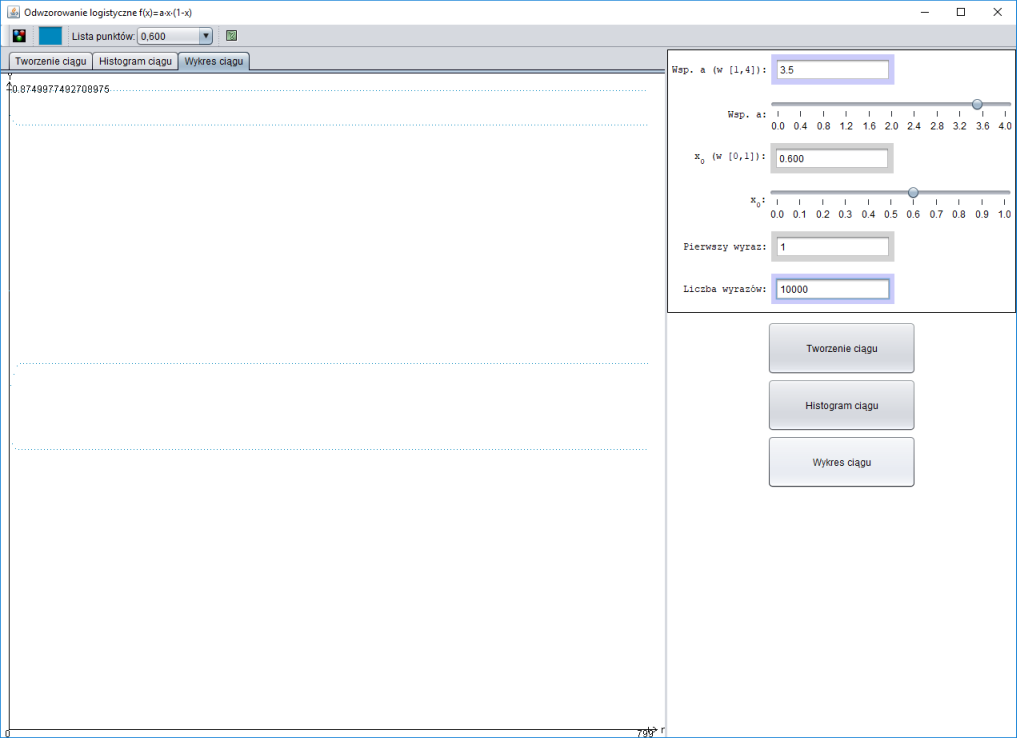
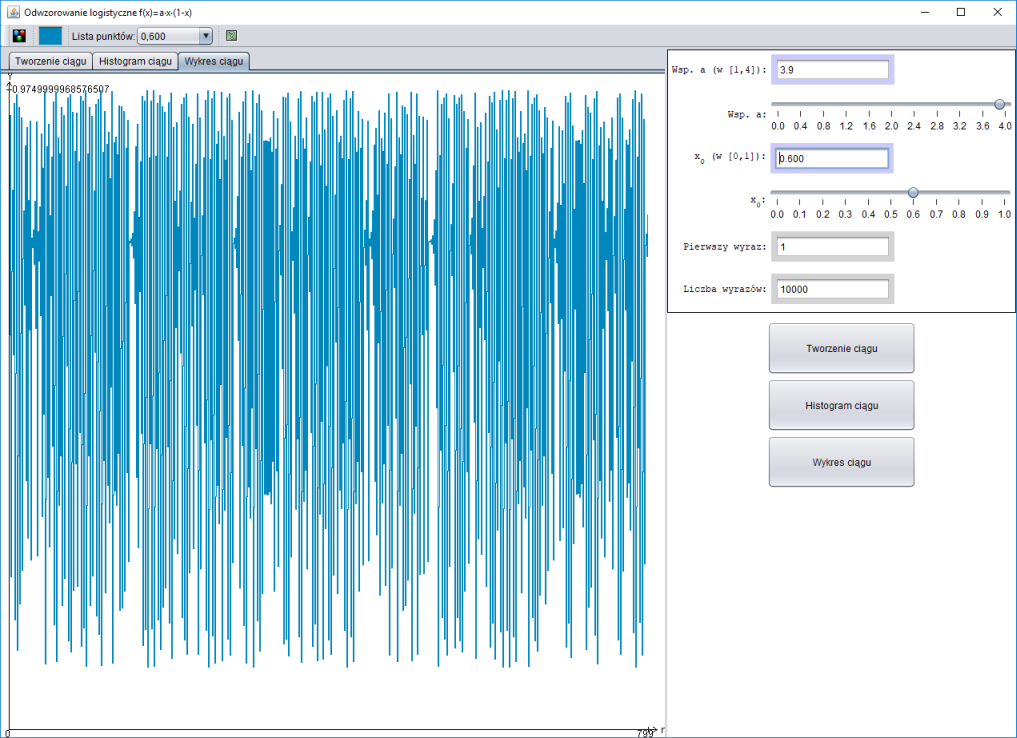
Rysunki można tworzyć programem LogisticMap. W zakładce Wykres ciągu widać tylko $800$ wyrazów ciągu, przeciągając myszą po wykresie można go przesuwać. Przeciągnięcie poza prawą krawędź przesuwa wykres do końca.

Wyobrażenie o wpływie współczynnika $a$ na zachowanie ciągu $(x_n)$ dają poniższe rysunki. Na każdym z nich dla $1001$ wartości współczynnika $a$ (zakres jest widoczny na osi $OX$) pokazano $10000$ wyrazów ciągu $(x_n)$. Na pierwszym rysunku są to początkowe wyrazy ciągu, na kolejnych są to wyrazy o numerach od $101$ do $10100$ – pominięcie pierwszych $100$ wyrazów powoduje iż oglądamy ciąg „ustabilizowany”.

Linia pozioma na powyższym rysunku jest konsekwencją tego, że każdy ciąg zawiera wyraz początkowy $0,2$.

Rysunki pokazują, że jeśli liczby $a$ spełniają (w przybliżeniu) nierówności $3,45 \le a \le 3,54$, to otrzymujemy ciąg czteroelementowy. Można „sprawdzić”, że jest to ciąg okresowy. Po kliknięciu w rysunek zobaczymy histogram ciągu (pokazujący, iż wyrazy ciągu występują równie często) i listę punktów potwierdzającą okresowość.
Do tworzenia rysunków można wykorzystać program Feigenbaum.

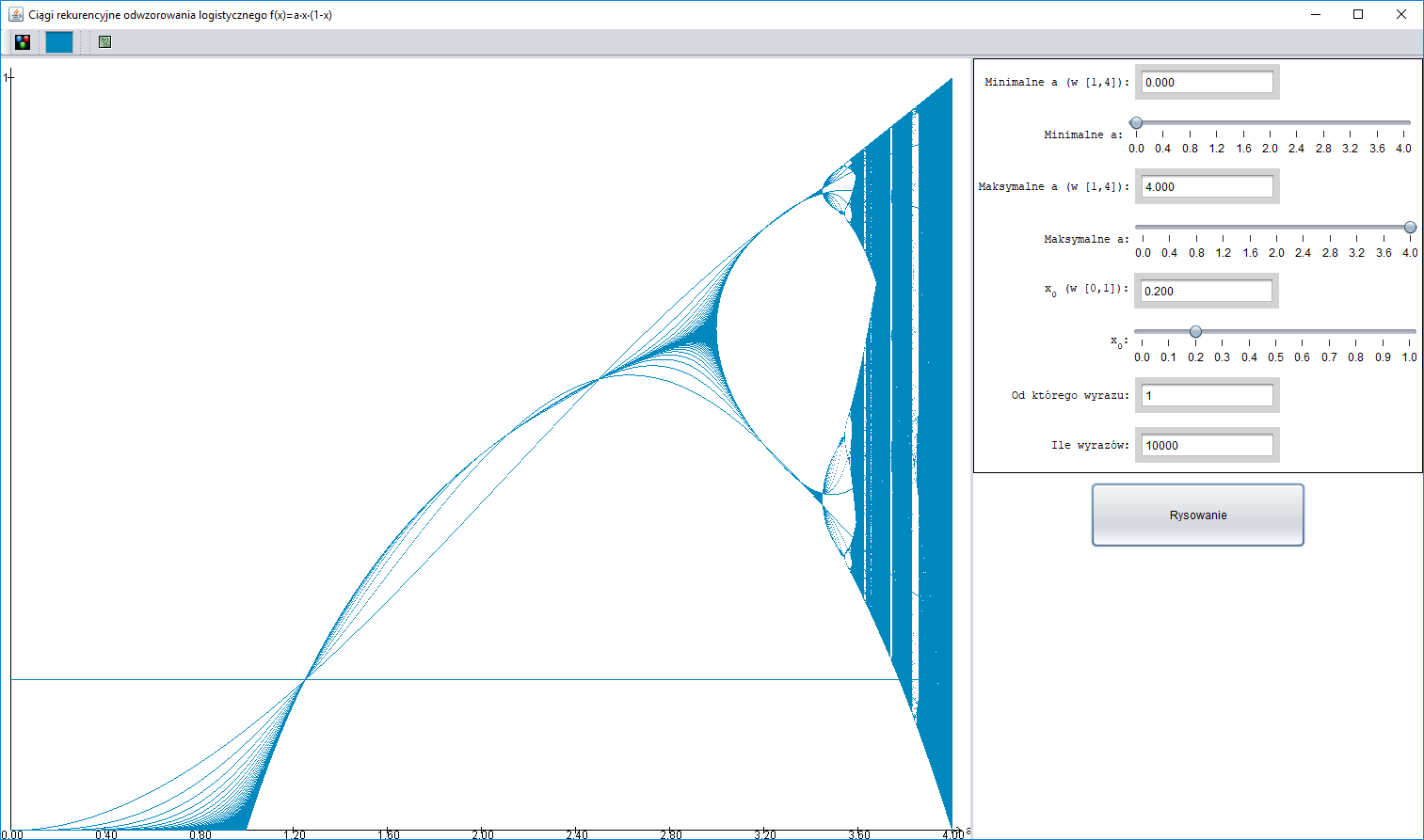
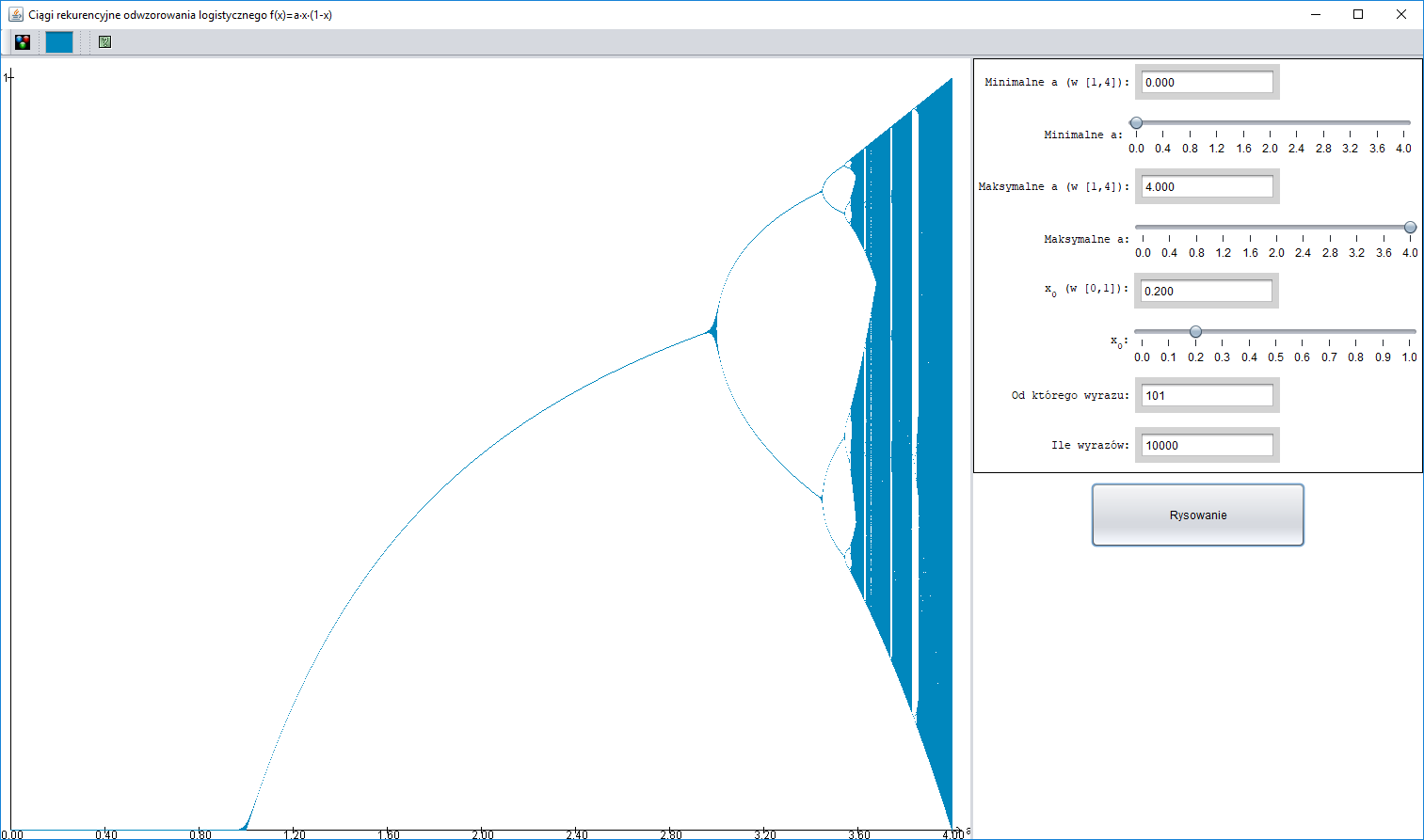
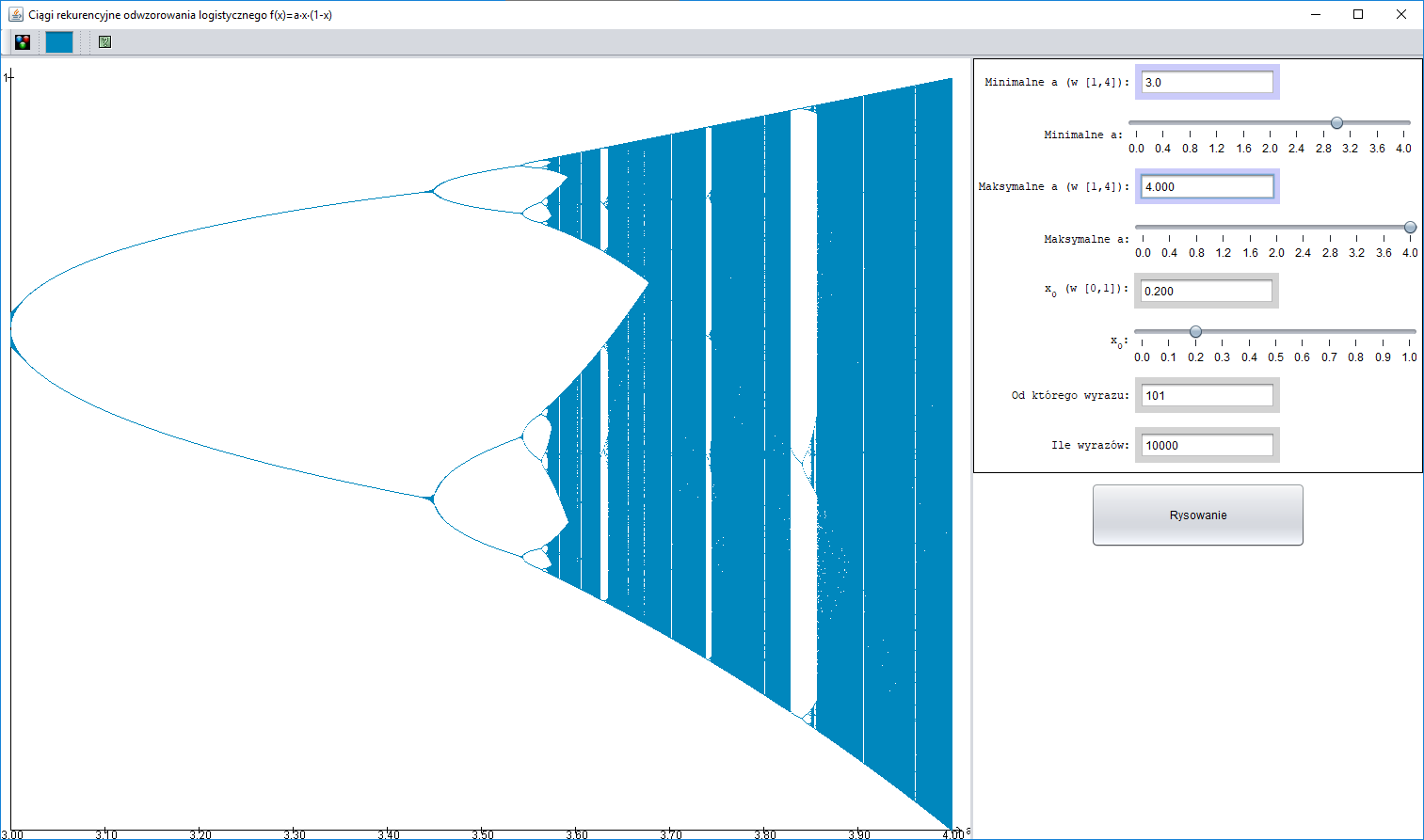
Można zauważyć wyspy porządku w morzu chaosu, podwojenie okresu dla pewnych wartości współczynnika $a$ oraz występowanie ciągów okresowych o bardzo różnych okresach. Zjawiska te są uniwersalne tzn. dotyczą szerokiej klasy funkcji – nie tylko funkcji $f_a(x) = ax(1 - x)$.

Twierdzenie Feigenbauma Jeżeli funkcje $f_a(x): [0;\, 1] \rightarrow [0;\, 1]$ zależne od parametru $a$ mają jedno (zależne od $a$) maksimum w punkcie $x_m(a)$, są rosnące na przedziale $[0;\, x_m(a)]$, malejące na przedziale $[x_m(a);\, 1]$, $f''_a(x_m) \ne 0$ oraz $\frac{f_a'''(x)}{f_a'(x)} \lt \frac{3}{2}\left( \frac{f_a''(x)}{f_a'(x)} \right)^2$ dla $x \ne x_>m(a)$, to istnieje ciąg $a_k \rightarrow g = 3,56995\ldots$, taki że dla każdej wartości $a_k$ następuje podwojenie okresu. Ponadto $\frac{g - a_{k-1}}{g - a_k} \rightarrow \mu = 4,6692016080\ldots$. Stała $\mu$ nazywana jest stałą Feigenbauma.
Mitchell Jay Feigenbaum

Odwzorowanie logistyczne (dla $a \gt 0$) spełnia założenia tw. Feigenbauma:

Rozważmy następujące uporządkowanie liczb naturalnych:
$3\prec 5\prec 7 \prec 9 \prec 11 \prec \ldots$
$2\cdot 3\prec 2\cdot 5 \prec 2\cdot 7 \prec \ldots$
$2^2\cdot 3 \prec 2^2 \cdot 5 \prec 2^2\cdot7 \prec \ldots$
$2^3\cdot 3 \prec 2^3 \cdot 5 \prec 2^3\cdot7 \prec \ldots$
$…$
$…\prec 2^5 \prec 2^4 \prec 2^3 \prec 2^2 \prec 2^1 \prec 2^0$
Najpierw są liczby nieparzyste $\gt 1$ w kolejności rosnącej, potem kolejno ich dwukrotności, czterokrotności, ośmiokrotności, … na końcu są (w kolejności malejącej) wszystkie potęgi liczby 2.

Twierdzenie Szarkowskiego Załóżmy że funkcja $f:[a;\, b] \rightarrow [a;\, b]$ jest ciągła. Jeśli dla pewnego punktu $x_0 \in [a;\, b]$ ciąg kolejnych iteracji $x_{n+1} = f(x_n)$ jest okresowy o okresie $m$ oraz liczba $m$ występuje w powyższym uporządkowaniu przed liczbą $k$, to istnieje taki punkt $y_0 \in [a;\, b]$, że ciąg kolejnych iteracji $y_{n+1} = f(y_n)$ jest okresowy o okresie $k$. W szczególności jeśli $m = 3$, to funkcja $f$ «generuje» ciągi okresowe o wszystkich możliwych okresach.
Ołeksandr Szarkowski

Uruchamianie programów

Wszystkie programy napisane są w Javie, do ich uruchomienia niezbędne jest zainstalowanie JRE (wersja $\ge 8$) JRE można pobrać stąd.
Linki na stronie prowadzą do plików zip lub jar. Ściągnięty plik zip należy rozpakować (w dowolnym katalogu), zawiera on plik jar i katalog resources z zasobami programu (pliki graficzne).
W systemie Windows program można uruchomić podwójnym kliknięciem w plik jar.
Lista programów: Sumy kontrolne MD5