Twierdzenia o punkcie stałym

Definicje

Załóżmy że $A$ jest pewnym zbiorem (np. podzbiorem $\mathbb{R}, \mathbb{R}^2, \mathbb{R}^3,\ldots, \mathbb{R}^n$), a przekształcenie (funkcja) $f$ odwzorowuje zbiór $A$ w siebie. Jeżeli $f(P) = P$, to mówimy że punkt $P$ ze zbioru $A$ jest punktem stałym odwzorowania $f$.

Twierdzenia o punkcie stałym mają natępującą postać: Jeśli zbiór $A$ jest „dostatecznie porządny”, to każde „dostatecznie regularne” przekształcenie $f:A \rightarrow A$ ma punkt stały. Każde twierdzenie o punkcie stałym, jest twierdzeniem o tym, że równanie (1) $f(x) = x$ ma rozwiązanie.

Twierdzenia o punkcie stałym mówią że, równanie (1) ma (dokładnie jedno) rozwiązanie. Dowody twierdzeń bywają konstruktywne (tzn. dające przepis na znajdowanie rozwiązania równania (1)) i niekonstruktywne.
Przykłady:

• $A = \mathbb{R}^2$, f jest przesunięciem o (niezerowy) wektor $w$, tzn. $f(x) = x + w$. Nie ma punktów stałych.
• $A = \mathbb{R}^2$, f jest obrotem wokół punktu $P$ o kąt nie bedący wielokrotnością $2\pi$. Punkt $P$ jest jedynym punktem stałym.
• $A = \mathbb{R}^2$, f jest symetrią względem prostej $l$, każdy punkt prostej $l$ jest punktem stałym.
• $A = $ koło jednostkowe, $f$ jest złożeniem $213$ odwzorowań z których każde jest przesunięciem, obrotem, symetrią lub jednokładnością dobranych tak, że dla każdego punktu $x$ z koła $A$ punkt $f(x)$ też należy do A. Istnieje punkt stały, chociaż jego istnienie nie jest oczywiste.

Zbiór $A$ nazywamy przestrzenią metryczną jeśli dla każdej pary punktów $x,y$ ze zbioru $A$> określona jest liczba nieujemna $d(x,y)$ nazywana odległością między $x$ a $y$ spełniająca warunki:

• $d(x,y) = d(y,x)$
• $d(x,x) = 0$
• $d(x,y \gt 0$, jeżeli $x \ne y$
• $d(x,y) + d(y,z) \le d(x,z)$, tzw. nierówność trójkąta

Przykłady: $\mathbb{R}, \mathbb{R}^2, \mathbb{R}^3, A_n = $ zbiór ciągów zero-jedynkowych o długości $n,\,\,d(x,y) = $ liczba pozycji na których ciągi $x$ oraz $y$ się różnią (tzw. odległość Hamminga używana w teorii kodowania).

Załóżmy, że $A$ jest przestrzenią metryczną, a punkty $x,x_1,\ldots,x_n,\ldots$ należą do zbioru $A$. Jeśli dla każdej liczby dodatniej $\delta\,\, d(x_n,x) \lt \delta$ dla prawie wszytkich liczb naturalnych $n$, to mówimy że ciąg $(x_n)$ jest zbieżny do punktu $x$.

Funkcja $f: A \rightarrow A$ jest ciągła jeśli dla każdego ciągu $(x_n)$ zbieżnego do $x$, ciąg $(f(x_n))$ jest zbieżny do $f(x)$.

Jeśli $A$ jest przestrzenią metryczną, $B$ jest podzbiorem $A$, to mówimy, że zbiór $B$ jest domknięty w $A$ jeśli dla każdego ciągu $(x_n)$ zawartego w zbiorze $B$ i zbieżnego do punktu $x$ ze zbioru $A$ punkt $x \in B$.

Przykłady:

• $B = (0; 1)$ nie jest domknięty w $\mathbb{R}$, ciąg $(\frac{1}{n})$ jest zawarty w $B$ i zbieżny do liczby $0$ która nie należy do $B$.
• $\mathbb{Q}$ nie jest domknięty w $\mathbb{R}$.

Dwa zbiory $A$ i $B$ zawarte w $\mathbb{R}^n$ są homeomorficzne jeśli istnieje wzajemnie jednoznaczne ciągła odwzorowanie $h: A \rightarrow B$ takie że odwzorowania odwrotne też jest ciągłe.

Twierdzenie Darboux

Jean Gaston Darboux

Jeśli funkcja $f:[a;\, b] \rightarrow \mathbb{R}$ jest ciągła, to dla każdej liczby $c$ leżącej między $f(a)$ i $f(b)$, równanie $f(x) = c$ ma rozwiązanie.

Wniosek Oznaczmy przez $S^1$ okrąg jednostkowy w $\mathbb{R}^2$. Dla każdego ciągłego odwzorowania $f:S^1 \rightarrow \mathbb{R}$ istnieje para punktów antypodycznych $x$ oraz $-x$ takich, że $f(x) = f(-x)$.

Dowód:
Definiujemy funkcję $h:[0;\, \pi] \rightarrow \mathbb{R}$ wzorem $h(t) = f(\cos(t);\, \sin(t))-f(-\cos(t),-\sin(t))$. Funkcja $h$ jest ciągła, $h(0) = f(1;\, 0) - f(-1;\, 0),\, h(\pi) = f(-1;\, 0) - f(1;\, 0) = -h(0)$.
Z tw. Darboux wynika iż istnieje w przedziale $[0;\, \pi]$ liczba $u$ taka że $h(u) = 0$. Wystarczy zauważyć że punkty $(\cos(u);\, \sin(u))$ oraz $(-\cos(u);\, -\sin(u))$ są antypodyczne.

Twierdzenie Brouwera o punkcie stałym

Jeśli zbiór $A$ zawarty w $\mathbb{R}^n$ jest ograniczony, wypukły i domknięty, to każda funkcja ciągłą $f:A \rightarrow A$ ma punkt stały.
Luitzen Brouwer udowodnił twierdzenie w 1911 roku.

Istnieje ogromna ilość dowodów (w większości niekonstruktywnych), około roku 1980 w czasopiśmie Lectures Notes in Economics pojawił się dowód konstruktywny.

Twierdzenie Brouwera jest równoważne z następującym (intuicyjnie bardziej oczywistym): Nie istnieje ciągłe odwzorowanie kuli (dowolnego wymiaru) na brzeg tej kuli, które pozostawia na miejscu wszystkie punkty brzegu.

Jeśli $n = 1$, to każdy zbiór ograniczony, wypukły i domknięty jest odcinkiem $[a;\, b]$. Ten szczególny przypadek twierdzenia Brouwera wynika z twierdzenia Darboux:
definiujemy funkcję $g:[a;\, b] \rightarrow \mathbb{R}$ wzorem $g(x) = f(x) - x$. Wtedy $g(a) = f(a) - a \ge 0,\,\, g(b) = f(b) - b \le 0$, z tw. Darboux wynika iż istnieje takie $x$ że $g(x) = 0$, tzn. $f(x) = x$.

Przykłady ilustrujące że wszystkie załozenia są istotne:

• zbiór $A$ nie jest domknięty: $A = (0;\, 1), f(x) = x^2$, funkcja $f$ nie ma (w $A$) punktu stałego,
• zbiór $A$ nie jest ograniczony: $A = \mathbb{R}, f(x) = x + 1$, funkcja $f$ nie ma punktu stałego,
• zbiór $A$ nie jest wypukły: $A = [-2;\, -1] \cup [1;\, 2], f(x) = -x$, funkcja f nie ma (w $A$) punktu stałego,

Nieoczekiwane konsekwencje twierdzenia Brouwera:

• jeżeli (pognieciony) plan Poznania rzucimy na ziemię w Poznaniu, to pewien punkt terytorium Poznania znajdzie się dokładnie pod swoim obrazem na planie,
• w każdej chwili czasu na każdym południku istnieją punkty antypodyczne, w których jest taka sama temperatura,
• dla każdych dwóch ograniczonych figur $A$ i $B$ leżących w jednej płaszczyźnie istnieje prosta $m$, która dzieli pole obu figur na pół

Twierdzenie Brouwera jest prawdziwe dla każdego zbioru $A$ zawartego w $\mathbb{R}^n$, który jest homeomorficzny ze zbiorem domkniętym, ograniczonym i wypukłym (taki zbiór sam jest domknięty i ograniczony, może nie być wypukły).
Twierdzenie Brouwera mówi o dowolnym zbiorze domkniętym, ograniczonym i wypukłym. Można prosto wykazać, że wystarczy je udowodnić dla jednego wybranego zbioru domkniętego, ograniczonego i wypukłego. W szczególności dla $n = 2$ wystarczy je udowodnić dla trójkata równobocznego.

Lemat 1 (Emanuel Sperner, 1928)

Jeśli ponumerujemy wierzchołki triangulacji trójkąta $A_1A_2A_3$ tak że wierzchołek $A_i$ ma numer $i$, wierzchołek leżący na boku $A_iA_j$ ma numer $i$ lub $j$, to istnieje trójkąt w pełni ponumerowany (tzn. o wierzchołkach z numerami 1,2,3).

Dowód:
Niech $r$ oznacza liczbę trókątów w pełni ponumerowanych.
Oznaczmy przez $S$ rodzinę boków o końcach 1 i 2. Na boku $A_1A_2$ leży nieparzysta ilość odcinków z rodziny $S$.
Niech $T$ oznacza dowolny trójkąt tworzący triangulację, $v(T)$ niech oznacza liczbę boków trójkąta $T$ należących do rodziny $S$. Liczba $v(T)$ jest nieparzysta wtedy i tylko wtedy gdy trójkąt $T$ jest w pełni ponumerowany. Zatem liczba $r$ jest nieparzysta wtedy i tylko wtedy gdy suma liczb (po wszystkich trójkątach) $v(T)$ jest nieparzysta. W sumie liczb $v(T)$ każdy odcinek z rodziny $S$ jest liczony dwa razy jeśli jest wspólnym bokiem dwóch trójkątów lub raz jeśli leży na boku $A_1A_2$. Zatem suma liczb $v(T)$ jest nieparzysta ⇒ liczba $r$ jest nieparzysta.

Lemat 2 (Sperner)

Jeśli trójkąt $A_1A_2A_3$ jest pokryty trzema zbiorami domkniętymi $Z_1,\, Z_2,\, Z_3$ w taki sposób że zbiór $Z_i$ jest rozłączny z bokiem leżącym naprzeciwko $A_i$ to zbiory $Z_1,\, Z_2,\, Z_3$ mają niepusty przekrój.

Dowód:
Dla dowolnej triangulacji numerujemy wierzchołki wg zasady: każdy wierzchołek dostaje numer zbioru $Z_i$ do którego należy (jeśli należy do paru, to wybieramy dowolnie). Istnieje wtedy (1-szy lemat Spernera) trójkąt w pełni ponumerowany. Bierzemy ciąg coraz drobniejszych triangulacji.

Dowód twierdzenia Brouwera dla trójkątów równobocznych

Dla każdego punktu $x$ należącego do trójkąta równobocznego $T$ o wierzchołkach $A_1,\,A_2,\,A_3$ oznaczmy przez $d_i(x)$ odległość od punktu $x$ do boku nie zawierającego wierzchołka $A_i$.

• $d_1(x) + d_2(x) + d_3(x) = \frac{1}{2}\sqrt{3}a$ gdzie $a$ jest długością boku trójkąta
• liczby nieujemne $a_1,\, a_2,\, a_3$ takie, że $a_1 + a_2 + a_3 = \frac{1}{2}\sqrt{3}a$ wyznaczają punkt w trójkącie

Załózmy że $f:T \rightarrow T$ jest funkcją ciągłą taką że $f(x) \ne x$ dla każdego $x$. Definiujemy zbiory $Z_i$ następująco: punkt $x$ należy do zbioru $Z_i$ jeżeli $d_i(f(x)) \le d_i(x)$ oraz różnica $d_i(x) - d_i(f(x))$ jest najmniejsza (punkt $x$ może należeć do paru zbiorów).

• każdy punkt gdzieś należy,
• zbiory $Z_i$ są domknięte,
• zbiór $Z_i$ jest rozłączny z bokiem przeciwległym do wierzchołka $A_i$,
• zbiory $Z_i$ mają pusty przekrój,

Sprzeczność z drugim lematem Spernera.

Odwzorowania zbliżające

Jeśli $A$ jest przestrzenią metryczną, $f:A \rightarrow A$ oraz istnieje liczba $0 \le q \lt 1$ taka, że dla każdych punktów $x,y$ ze zbioru $A\,\, d(f(x),f(y)) \le qd(x,y)$ to mówimy że odwzorowanie $f$ jest zbliżające (jest kontrakcją).

Twierdzenie o odwzorowaniu zbliżającym (Twierdzenie Banacha o kontrakcji, Stefan Banach).
Jeśli zbiór $A$ zawarty w $\mathbb{R}^n$ jest domknięty oraz odwzorowanie $f:A \rightarrow A$ jest kontrakcją, to odzworowanie $f$ ma dokładnie jeden punkt stały $\tilde{x}$. Dla każdego punktu $x_0$ ze zbioru $A$ ciąg określony rekurencyjnie $x_{n+1} = f(x_n)$ jest zbieżny do punktu stałego $\tilde{x}$ oraz $d(\tilde{x},x_n) \le \frac{q^n}{1-q}(d(x_1,x_0)$.
Przykłady:

• $A =$ zbiór liczb $\ge 1$, $f:A \rightarrow A,\, f(x) = x + \frac{1}{x}$, funkcja $f$ spełnia nierówność $d(f(x),f(y)) \lt d(x,y)$, ale nie jest odwzorowaniem zbliżającym (i nie ma punktu stałego).
• $A = [0; 1],\, f:A \rightarrow A, f(x) = \cos(x)$, $f$ jest zbliżająca zatem ciąg: $0,\cos(0),\cos(\cos(0)),\ldots$ jest zbieżny do (jedynego) rozwiązania równania $\cos(x) = x$.
• Równanie $2x + \sin(x) = 1$, szukamy rozwiązania z dokładnością do $0,1$, przepisujemy równanie do postaci $x = \frac{1-\sin(x)}{2}$, odwzorowanie $f:\mathbb{R} \rightarrow \mathbb{R},\, f(x) = \frac{1-\sin(x)}{2}$ jest zbliżające:
  $|f(x) - f(y)| = \frac{|\sin(x) - \sin(y)|}{2} = |\frac{\sin(x-y)}{2}||\frac{\cos(x+y)}{2}| \le |\frac{\sin(x-y)}{2}| \le \frac{|x-y|}{2},\, x_0 = 0,\, x_1 = f(x_0) = 0.5$, wystarczy zatem obliczyć $x_4$.

Odwozorowania Hutchinsona

Twierdzenie Banacha o kontrakcji jest prawdziwe dla znacznie obszerniejszej klasy przestrzeni metrycznych niż zbiory domknięte w $\mathbb{R}^n$.
Omówię jeden przykład mocno związany z fraktalami.

Jeśli $A$ jest podzbiorem domkniętym płaszczyzny, a punkt $x$ leży na płaszczyźnie, to symbolem $d(x, A)$ oznaczamy odległość od punktu $x$ do najbliższego punktu zbioru $A$. Nazywamy tą liczbę odległością punktu $x$ od zbioru $A$.
Jeśli $A$ jest podbiorem płaszczyzny oraz liczba $r \gt 0$, to $A_r$ oznaczać będzie „nadmuchany” zbiór $A$, tzn. sumę wszystkich kół o promieniu $r$ i środku należącym do zbioru $A$.

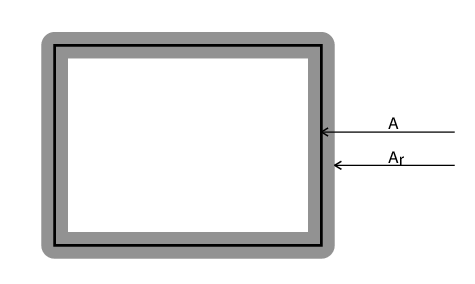
Oznaczmy przez $m(A,B)$ najmniejszą liczbę (dokładniej kres dolny) $r \gt 0$ o tej własności że $B \subset A_r$, analogicznie określamy liczbę $m(B,A)$. Odległością Hausdorffa (Felix Hausdorff) zbiorów $A$ i $B$ nazywamy większą z tych liczb: $d(A,B) = \max(m(A,B), m(B,A))$. Tak określona odległość spełnia warunki przestrzeni metrycznej.

Przykład: $A$ jest kwadratem o boku $s$, $B$ jest kołem wpisanym w kwadrat $A$. Dla każdego punktu $x$ z koła $B\,\, d(x,A) = 0$. Dla punktów $y$ z kwadratu $A$ odległość $d(y,B)$ jest największa wtedy gdy $y$ jest wierzchołkiem kwadratu i wynosi wtedy $\frac{\sqrt{2}s - s}{2}$. Zatem $d(A,B) = \frac{\sqrt{2}s - s}{2}$.

Dla przestrzeni metrycznej utworzonej z niepustych, domkniętych i ograniczonych podzbiorów płaszczyzny prawdziwe jest twierdzenie o odwzorowaniu zbliżającym. W dalszym ciągu będę tą przestrzeń metryczną oznaczał $F$.

Odwzorowanie $f:\mathbb{R}^2 \rightarrow \mathbb{R}^2$ nazywamy odwzorowaniem afinicznym jeśli jest postaci $f(x, y) = (ax + by + c, dx + ey + g)$. Równoważne – geometryczne – określenie: obrazem każdej prostej jest prosta lub punkt. Definicja ta obejmuje przesunięcia, obroty, symetrie, jednokładności, rzutowania, odbicia oraz złożenia wymienionych odwzorowań.

Jeśli odwzorowania $f_1,\ldots,f_k:\mathbb{R}^2 \rightarrow \mathbb{R}^2$ są afiniczne, to odwzorowanie: $H:F \rightarrow F,\,\, H(A) = f_1(A) \cup\ldots\cup f_k(A)$ nazywamy odwzorowaniem Hutchinsona (John E. Hutchinsona, Australia 1981). Można pokazać że jeśli każde z odwzorowań afinicznych $f_1,\ldots,f_k$ jest zbliżające (ze względu na „zwyczajną” metrykę na płaszczyźnie) to wyznaczone przez nie odwzorowanie Hutchinsona jest odwzorowaniem zbliżającym (ze względu na odległość Hausdorffa). Przykład:

• $f_1(x, y) = (\frac{x}{2}, \frac{y}{2})$, jednokładność o skali $0,5$
• $f_2(x, y) = (\frac{x}{2}, \frac{y}{2}) + (\frac{1}{2}, 0)$, złożenie jednokładności o skali $0,5$ i przesunięcia w prawo
• $f_3(x, y) = (\frac{x}{2}, \frac{y}{2}) + (\frac{1}{4}, \frac{\sqrt{3}}{4})$, złożenie jednokładności o skali $0,5$ i przesunięcia na ukos, w prawo i do góry

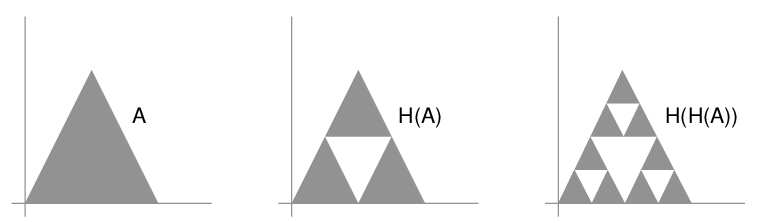
Wybieramy zbliżające odwzorowania afiniczne płaszczyzny $f_1,\ldots,f_k$ i tworzymy przy ich pomocy odwzorowanie Hutchinsona $H$. Wybieramy dowolny niepusty, domknięty i ograniczony podzbiór płaszczyzny (może to być zbiór jednopunktowy) $Z_0$. Ciąg zbiorów $Z_1 = H(Z_0),\ldots,Z_{n+1} = H(Z_n),\ldots$ jest zbieżny do pewnego zbioru $A$ (niezależnego od wyboru zbioru $Z_0$). Zbiór $A$ nazywamy atraktorem odwzorowania $H$. Atraktor spełnia równanie $H(A) = A$.

Atraktory pewnych odwzorowań Hutchinsona $H$ mają bardzo atrakcyjny wygląd. Dla odwzorowania $H$ z powyższego przkładu, atraktorem jest trójkąt Siepińskiego: